- #1
LCSphysicist
- 645
- 161
- Homework Statement
- I will post below
- Relevant Equations
- There is no
I just found a definition to the Young modulus as:
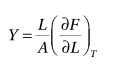
Is this a plausible representation of Y? That is, i know the definition
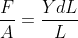 , i don't think we can say this definition and the first definition is equal.
, i don't think we can say this definition and the first definition is equal.
Is this a plausible representation of Y? That is, i know the definition