Find a circle inside of and tangent to a larger circle

[Ventrella]

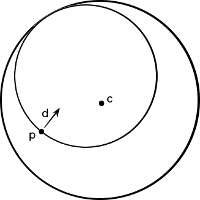
Start with a circle of radius r and center c. Inside of that circle is an arbitrary point p. Given an arbitrary normalized direction vector d, I need to find the radius and center the circle that (1) intersects p, (2) is tangent with the circle centered at c, and (3) has its center lying on the ray originating at p and aimed in direction d. The image below shows an example of a smaller circle that meets these constraints. I suspect the solution involves at least one dot product involving c, p, and d...but I cannot come up with an elegant solution. Any suggestions? Thanks! - Jeffrey

 

[andrewkirk]

I don't know about elegant, but the following procedure should give a route to a solution:

We know points $\dot c,\dot p$, scalar radius $r$ and unit vector $\vec d$. I've put dots over the symbols for geometric points to differentiate them from vectors and scalars. Note that subtracting points (eg $\dot p-\dot c$) gives a vector, and adding a vector to a point (eg $\dot b+\vec d$) gives a new point. We can think of vectors as displacements of points.

Let the centre and radius of the new circle be point $\dot f$ and scalar $s$.
Those are two unknowns, so we want to find two equations involving them, that we can then solve.

Using the subtraction and addition described above,

• we can write one equation expressing $\dot f$ in terms of $\dot p, \vec d$, and $s$, based on the requirement that $\dot f$ is in direction $\vec d$ from $\dot p$ (how far in that direction?); and
• we can write another equation based on the triangle of vectors formed by $(\dot p-\dot c),\ (\dot f-\dot p)$ and $(\dot c-\dot f)$ and equating the length of that third vector to a formula involving only $r$ and $s$, that we can deduce from a carefully-drawn diagram.

Hopefully that's enough of a hint. To say more might spoil the fun.

 

[votingmachine]

I don't know about elegant, but the following procedure should give a route to a solution:

We know points $\dot c,\dot p$, scalar radius $r$ and unit vector $\vec d$. I've put dots over the symbols for geometric points to differentiate them from vectors and scalars. Note that subtracting points (eg $\dot p-\dot c$) gives a vector, and adding a vector to a point (eg $\dot b+\vec d$) gives a new point. We can think of vectors as displacements of points.

Let the centre and radius of the new circle be point $\dot f$ and scalar $s$.
Those are two unknowns, so we want to find two equations involving them, that we can then solve.

Using the subtraction and addition described above,

• we can write one equation expressing $\dot f$ in terms of $\dot p, \vec d$, and $s$, based on the requirement that $\dot f$ is in direction $\vec d$ from $\dot p$ (how far in that direction?); and
• we can write another equation based on the triangle of vectors formed by $(\dot p-\dot c),\ (\dot f-\dot p)$ and $(\dot c-\dot f)$ and equating the length of that third vector to a formula involving only $r$ and $s$, that we can deduce from a carefully-drawn diagram.

Hopefully that's enough of a hint. To say more might spoil the fun.

Would that work for the special case where point $\dot p$ is not triangular to the large circle center $\dot c$? My instinctive starting simplification was to think of the special case where $\vec d$, $\dot p$, $\dot p$, and the tangential intersection all line up nicely.

I see the logic in your answer, but I realized the triangle is a line in that special case (where $r$ and $s$ are more obvious) . And that confuses me.

 

[Ventrella]

Thanks Andrew! Since you gave a hint and mentioned "not spoiling the fun", I see you are interested in the process of discovery. Your hint indicates that there may be trigonometry involved.

As more fodder for thought, I had previously tried to simplify the problem by rotating my view such that d always aims upward. I got a suspicion that a new value b might be useful, which I generated by plotting a point on the large circle at the bottom. In doing so, I gained an intuition that the radius of the small circle should be inversely proportional to the gradient of nested radii - as shown in the picture below at right.

As per VotingMachine's response, I imagine the case where all the points line up in the middle vertical axis in my diagram as enabling a simple linear result, with the radius of the small circle being r at the bottom and 0 at the top. With this in mind, I assume that there is a scalar value that takes into account p extending to the left or right of the center axis, being zero at the extreme left and right sides of the large circle. I suspect this can be calculated from a dot product, but am not yet sure which vectors to use. Perhaps your hint will help me discover the answer.

I will noodle on this. I just wanted to add my previous explorations - to make it more fun!
Thanks,
-j

 

[andrewkirk]

Would that work for the special case where point $\dot p$ is not triangular to the large circle center $\dot c$?

I expect not. That is a 'degenerate case', meaning that there are an infinite number of solutions, rather than only one. The ray on which $\dot f$ lies is an extension of a radial line of the original circle. For any point on that ray, there is a circle centred at that point that is tangent to the original circle.

Hence, in order to exclude the degenerate case, we need to preface the solution strategy above by a test as to whether there exists scalar $\lambda$ such that $\dot c-\dot f=\lambda\vec d$ or, alternatively, $(\dot c - \dot f)\cdot \vec d = \|\dot c - \dot f\|\ \|\vec d\|$.

 

[mfb]

I expect not. That is a 'degenerate case', meaning that there are an infinite number of solutions, rather than only one.

I don't see how you can find more than one solution in this case.

Hence, in order to exclude the degenerate case, we need to preface the solution strategy above by a test as to whether there exists scalar $\lambda$ such that $\dot c-\dot f=\lambda\vec d$ or, alternatively, $(\dot c - \dot f)\cdot \vec d = \|\dot c - \dot f\|\ \|\vec d\|$.

This scalar has to exist for all problems. $\vec d$ points from c into the direction of f.

@Ventrella: A sketch where f is drawn (together with relevant connections between the different points) will help a lot.

 

[andrewkirk]

I don't see how you can find more than one solution in this case.This scalar has to exist for all problems. $\vec d$ points from c into the direction of f.

As I read the OP, $\vec d$ points from $\dot p$ (not $\dot c$) in the direction of $\vec f$.

 

[mfb]

Ah, I misread your c as p.

Anyway, this special case is just easier, it is not degenerate.

 

[Baluncore]

This is an interesting problem. If p(x,y) is within the outer circle, then there is a solution.
The geometry is the intersection of a ray with the surface of a cone, at the point t(x,y).
The outer circle, centred at c(x,y), is the base of the cone with radius = r = height.
The ray starts on the cone base at p(x,y), in the direction β, rising with a slope of 1.

To find the centre of the small circle, t(x,y), we have a parameter t = the radius of the small circle.
That is the horizontal distance from p(x,y) to t(x,y) = r – distance from c(x,y) to t(x,y).

tx = px + t * Cos( β )
ty = py + t * Sin( β )
t = r – √( (cx–tx)² + (cy–ty)² )

Note, the vertical plane containing the ray cuts the cone as a hyperbola.
The horizontal distance from p(x,y) to the ray crossing the hyperbola is t.
Maybe that is another way to solve it.

 

[Ventrella]

I’m still noodling on the idea I suggested earlier. If I’m on the right track, I assume my solution maps to the two other solutions proposed. I suspect the blue map of circles in the diagram below is analogous to the cone proposed by Baluncore. Let me know if this makes sense.

 

[andrewkirk]

Why do you think that approach would give a correct answer?

 

[Ventrella]

Why do you think that approach would give a correct answer?

Well - the math works out! Check out this video...

http://fractalcurves.com/test.mp4

The video shows a test I whipped up in JavaScript (to prove to myself that it works).

I determine the length of chord bg (which was missing from the algorithm described earlier) by normalizing the vector from b to p, dotting it with the direction vector, and then scaling it by r times 2.

What's cool is that I was able to do it all without any trig/angles :)
-j

 

[Ventrella]

I discovered that the smaller circle has a similar triangle as in the large circle, by connecting the dots.

(I tilted the direction by 45 degrees in this example)

Here's a video showing the same thing in motion...

http://www.fractalcurves.com/similar_triangles.mp4

I can't say for sure, but does this reveal a connection to the solution you suggested @andrewkirk ?
-j

 

[andrewkirk]

does this reveal a connection to the solution you suggested @andrewkirk ?
-j

Yes, that appears to validate the method you proposed above.

 

[Baluncore]

Here is my vector solution.

Input variables;
Vector c = Type( -1, -1 ) ' big circle centre( x, y )
Double r = 4 ' big circle radius

Vector p = Type( -0.1, 2 ) ' position( x, y ) of director
Double beta = 4.7 ' direction of director d in radians
Vector d = Type( Cos(beta), Sin(beta) ) ' director d is a unit vector

process;
Vector u = p - c ' translate diagram to make big circle centre origin
u = u * conj( d ) ' point director from p towards +x

' find radius and distance from p along director to small circle centre
Double t = ( r^2 - u.x^2 - u.y^2 ) / ( 2 * ( r + u.x ) ) ' magic

Vector s = p + ( t * d ) ' s is the centre of the small circle, with radius t.

 

[votingmachine]

I discovered that the smaller circle has a similar triangle as in the large circle, by connecting the dots.

(I tilted the direction by 45 degrees in this example)

View attachment 212036

Here's a video showing the same thing in motion...

http://www.fractalcurves.com/similar_triangles.mp4

I can't say for sure, but does this reveal a connection to the solution you suggested @andrewkirk ?
-j

When I drew it I could not prove to myself that the chord which goes from $\dot b$ to $\dot p$ to $\dot g$ is the tangent point. Once you know that, the large circle radius, $\dot c$ to $\dot f$ to $\dot g$ and the chord form a triangle.

It looks that way in the drawing, but how did you prove that chord terminus and tangent point are the same?

 

[Ventrella]

When I drew it I could not prove to myself that the chord which goes from $\dot b$ to $\dot p$ to $\dot g$ is the tangent point. Once you know that, the large circle radius, $\dot c$ to $\dot f$ to $\dot g$ and the chord form a triangle.

It looks that way in the drawing, but how did you prove that chord terminus and tangent point are the same?

Hi @votingmachine ,

Good question. I came up with my solution based on intuition and testing, and I do not have a proof.

I am assuming that the solutions that you and others have proposed are based on trigonometry. Since I am not well-versed in trig, I found a different way to express the solution, which I believe is correct, but I have no proof.

If my solution could be shown to be equivalent to a trig-based solution, then would that be a sufficient proof? I have used a dot product, which is related to cosines. Would this be a clue?
-j

 

[andrewkirk]

When I drew it I could not prove to myself that the chord which goes from $\dot b$ to $\dot p$ to $\dot g$ is the tangent point.

It follows from the diagram in post 13, which shows the solution. Two marked points in the diagram are unlabelled. Label the leftmost as b and the rightmost as g. The triangles bcg and pfg are similar, so pf is parallel to bc. Now rotate the diagram so that b is at the bottom. Then we can see that the marked points correspond to those in the diagram in post 10 with dots over them. In particular, the line from $\dot b$ through $\dot p$ goes through $\dot g$.

 

[votingmachine]

It follows from the diagram in post 13, which shows the solution. Two marked points in the diagram are unlabelled. Label the leftmost as b and the rightmost as g. The triangles bcg and pfg are similar, so pf is parallel to bc. Now rotate the diagram so that b is at the bottom. Then we can see that the marked points correspond to those in the diagram in post 10 with dots over them. In particular, the line from $\dot b$ through $\dot p$ goes through $\dot g$.

I see the diagram. My question is why is it not drawn such that there are TWO rightmost points. One that is the endpoint of $\dot c$ to $\dot f$ which ends at $\dot k$, and one that is the endpoint of $\dot b$ to $\dot p$ which ends at $\dot g$. That drawing would have 4 points, not 3.

I see why drawing it with the tangent point being the same point as the chord terminal point FITS. It does look right.

 

[Ventrella]

I see the diagram. My question is why is it not drawn such that there are TWO rightmost points. One that is the endpoint of $\dot c$ to $\dot f$ which ends at $\dot k$, and one that is the endpoint of $\dot b$ to $\dot p$ which ends at $\dot g$. That drawing would have 4 points, not 3.

I see why drawing it with the tangent point being the same point as the chord terminal point FITS. It does look right.

Here's an updated diagram with extensions of the two radii to make two diameters - drawn in blue. I labeled them k1 and k2. It reveals another pair of similar triangles. Any lines that reveal similar triangles should be enough to express (or inspire) a solution to the problem.

 

[votingmachine]

Here's an updated diagram with extensions of the two radii to make two diameters - drawn in blue. I labeled them k1 and k2. It reveals another pair of similar triangles. Any lines that reveal similar triangles should be enough to express (or inspire) a solution to the problem.

View attachment 212360

I don't think that is quite the proof I was looking for. I'm not sure if I was clear. The question I had was how do we know the line from $\dot b$ to $\dot p$ ends at the tangent point $\dot g$, and not another point on the large circle. If it is shown they are the same point, then the similar triangles completes the radius derivation.

I don't disbelieve they are the same point. The drawings line up and it FITS. Every drawing (and the helpful MP4 graphic) LOOKS right. I just don't quite see why.

 

[andrewkirk]

@votingmachine Start with the diagram with $\dot c,\dot p, \vec d$ marked, and let $\dot f,\dot g$ be the centre and tangent point of the circle that is the solution. Now define $\dot b$ to be the point where the line from $\dot g$ through $\dot p$ crosses the circle again.

Then we can easily show that the triangles $\dot g\dot b\dot c$ and $\dot g\dot p\dot f$ are similar (since both are isosceles, and they share an angle), from which it follows that $\dot b\dot c$ is parallel to $\dot p\dot f$, which is parallel to $\vec d$.

So, to find this solution, all we need do is

1. find the point $\dot b$ where the line through $\dot c$ parallel to $\vec d$ but in reverse direction cuts the circle
2. find the point $\dot g$ where the line from $\dot b$ through \dot p## cuts the circle again. That is the tangent point
3. find the point $\dot f$ where the radius from $\dot g$ to $\dot c$ cuts the ray in direction $\vec d$ from $\dot p$. That is the centre of the smaller circle.

which is the approach Ventrella described - albeit in slightly different words..

 

[votingmachine]

Got it. That method explicitly draws triangles, and they are similar. Thanks.

 

[Baluncore]

The question I had was how do we know the line from ˙b\dot b to ˙p\dot p ends at the tangent point ˙g\dot g, and not another point on the large circle.

B–K1 is a diameter of the big circle. Thales' theorem gives the angle at G between B and K1 as 90°.
P–K2 is a diameter of the small circle. Thales' theorem gives the angle at G between P and K2 as 90°.
Since the diameters B–K1 and P–K2 are parallel, and the angles at G are the same, the point K2 must lie on the small circle and they must be similar triangles.