- #1
Astrowolf_13
- 1
- 1
- Homework Statement
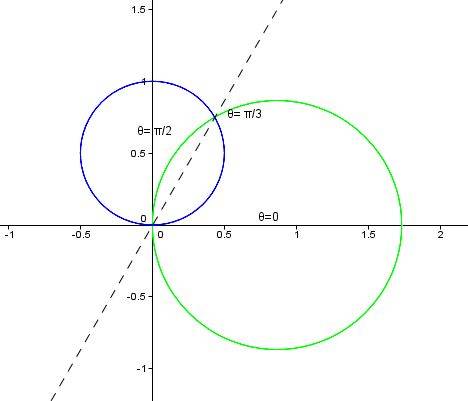
- Find the area limited by polar curves ##r=sin(\theta)## and ##r=\sqrt 3*cos(\theta)##.
- Relevant Equations
- ##r=sqrt(3)*cos(\theta)##, ##r=sin(\theta)##, ##0 \leq \theta \leq pi/2##.
I attempted to solve this problem by finding the angles of an intersection point by equalling both ##r=sin(\theta)## and ##r=\sqrt 3*cos(\theta)##. The angle of the first intersection point is pi/3. The second intersection point is, obviously, at the pole point (if theta=0 for the sine curve and theta=pi/2 for the cosine curve). I then attempted to find the required area by summing its "parts":
$$Area=0.5*\int_0^\frac{\pi}{3} (sin(\theta))^2\, d(\theta) + 0.5*\int_\frac{\pi}{3}^\frac{\pi}{2} (\sqrt 3 *cos(\theta))^2\, d(\theta)$$
The final area I got is ##5*\pi/24 + \sqrt 3 /4##, which I checked on the Internet. However, my teacher disregarded this solution as incorrect (because, as I quote, line at angle pi/3 is not a boundary of either ##r=sin(\theta)## or ##r=\sqrt 3 *cos(\theta)##) and asked to use a different method to find the area, and this is what I'm struggling to do.
So the question is: is there any other method of finding this area or did I get the description of the homework statement wrong?
The graph should look like this:
$$Area=0.5*\int_0^\frac{\pi}{3} (sin(\theta))^2\, d(\theta) + 0.5*\int_\frac{\pi}{3}^\frac{\pi}{2} (\sqrt 3 *cos(\theta))^2\, d(\theta)$$
The final area I got is ##5*\pi/24 + \sqrt 3 /4##, which I checked on the Internet. However, my teacher disregarded this solution as incorrect (because, as I quote, line at angle pi/3 is not a boundary of either ##r=sin(\theta)## or ##r=\sqrt 3 *cos(\theta)##) and asked to use a different method to find the area, and this is what I'm struggling to do.
So the question is: is there any other method of finding this area or did I get the description of the homework statement wrong?
The graph should look like this:
Last edited: