Force on a dipole from a point charge

[BigTanker]

Homework Statement

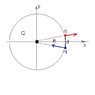
A point charge, Q, is "nailed down" on a table. Around it, at radius R, is a frictionless circular track on which a dipole $\boldsymbol{p}$ rides, constrained to always point tangent to the circle. Show that the electric force on the dipole is (in the forward direction of the dipole):$$\boldsymbol{F} = \frac{Q}{4 \pi \epsilon_0} \frac{\boldsymbol{p}}{R^3}$$

Homework Equations

$$\boldsymbol{F} = ( \boldsymbol{p} \cdot \nabla ) \boldsymbol{E}$$

The Attempt at a Solution

I started by recognizing that the electric field from the point charge is $$\boldsymbol{E} = \frac{1}{4 \pi \epsilon_0} \frac{Q}{R^2} \hat{r}.$$

Thus, I feel like the force should be: $$\boldsymbol{F} = ( \boldsymbol{p} \cdot \nabla ) \boldsymbol{E} = \boldsymbol{p} \frac{-2}{4 \pi \epsilon_0} \frac{Q}{R^3} = \frac{-Q}{2 \pi \epsilon_0} \frac{\boldsymbol{p}}{R^3}.$$

However, if I draw the dipole out as 2 separated point charges, +q and -q, I see that the net force should point in the direction as the dipole, not opposite the direction of the dipole (as my math above would suggest).

Where have I erred?

 

[BigTanker]

I've found that I can reach the answer using the expression for torque, $\boldsymbol \tau = \boldsymbol p \times \boldsymbol E = |\boldsymbol p | |\boldsymbol E | (-\hat{\phi})$, and that $|\boldsymbol F | = \frac{|\boldsymbol \tau |}{R}.$

Therefore, $$\boldsymbol F = \frac{|\boldsymbol p | |\boldsymbol E |}{R} \hat{p} = \frac{\boldsymbol p |\boldsymbol E |}{R} = \frac{Q}{4 \pi \epsilon_0} \frac{\boldsymbol p}{R^3}.$$

Of course, I'm making the educated assumption that $\boldsymbol F$ is in the $\boldsymbol p$ direction. However, the problem states that I should use the equation $\boldsymbol{F} = ( \boldsymbol{p} \cdot \nabla ) \boldsymbol{E}$ to show my result (as opposed to using the straightforward method of manipulating the torque, above).

 

[BigTanker]

I also realized that in my initial attempt at a solution, that I was taking the gradient of E as opposed to the divergence of $\boldsymbol E$. So, taking the divergence gives me $$\boldsymbol F (r) = \boldsymbol p \frac{1}{r^2} \frac{\partial r^2 E}{\partial r} = \frac{\boldsymbol p}{4 \pi \epsilon_0 R^2 r^2} \frac{\partial r^2}{\partial r} = \frac{\boldsymbol p 2 r}{4 \pi \epsilon_0 R^2 r^2} = \frac{\boldsymbol p}{2 \pi \epsilon_0 R^2 r}$$

Evaluated at r=R, $$\boldsymbol F = \frac{\boldsymbol p}{2 \pi \epsilon_0 R^3},$$ which is in the proper direction now, but still off by a factor of 2...

 

[ehild]

Just determine the resultant of the Coulomb forces acting on the dipole, considering it two opposite point charges d distance apart.

ehild

 

[Stealth95]

I think that ehild proposed the easiest approach for this problem. But note that using Coulomb's law you can find the force only for the case in which the dipole is in this specific point of space. If you move the dipole in another place then you must apply Coulomb's law again to find the new force.

If you use the equation you said you can find the general equation for the force (for any point). But it is not correct to find $\displaystyle{\nabla \cdot \vec{E}}$. The operator is not $\displaystyle{\nabla \cdot }$ but $\displaystyle{\vec{p} \cdot \nabla}$. So you must find $\displaystyle{\vec{p} \cdot \nabla}$ first.

 

[BigTanker]

@Stealth and ehild: I should have stated in my OP explicitly that the problem wanted me to use the equation $\boldsymbol F = (\boldsymbol p \cdot \nabla ) \boldsymbol E$.

I see where my math error was, but if I think about it that way, it seems that $\boldsymbol p \cdot \nabla$ is a scalar, thus the force will point in the direction of $\boldsymbol E$, which is in the $\hat{r}$ direction, which is incorrect...

Since $\boldsymbol p = p \hat{\theta} = p_\theta$, then $p_r = p_\phi = 0$ and:$$\boldsymbol p \cdot \nabla = \frac{1}{r \sin \theta} \frac{\partial}{\partial \theta} (p \sin \theta) = \frac{p}{r \sin \theta} \frac{\partial}{\partial \theta} (\sin \theta).$$

Then, $$\boldsymbol F = ( \boldsymbol p \cdot \nabla ) \boldsymbol E = \frac{p}{r \sin \theta} \frac{\partial (\frac{Q}{4 \pi \epsilon_0 R^2} \hat{r} \sin \theta)}{\partial \theta} = \frac{-p Q \cos \theta}{4 \pi \epsilon_0 R^3 \sin \theta} \hat{r}= \frac{-p Q \cot \theta}{4 \pi \epsilon_0 R^3} \hat{r}.$$

That's my attempt thus far; I'm not really sure where I've misstepped.

(edit: I found some hideous expression on wikipedia for $(\boldsymbol A \cdot \nabla ) \boldsymbol B$. Which, when I reduce it using $p_r = p_\phi = E_\theta = E_\phi = 0$ and $E_r = f(r)$, yields the simple expression $$\frac{p_\theta E_r}{r} \hat{\theta},$$ which gives me the answer I'm looking for. Apparently when I try to explicitly find $( \boldsymbol p \cdot \nabla ) \boldsymbol E$, I'm making some math error along the way...)

 

[ehild]

You can understand it better in Cartesian coordinates. See http://web.mit.edu/6.013_book/www/chapter11/11.8.html

ehild

 

[vela]

@Stealth and ehild: I should have stated in my OP explicitly that the problem wanted me to use the equation $\boldsymbol F = (\boldsymbol p \cdot \nabla ) \boldsymbol E$.

I see where my math error was, but if I think about it that way, it seems that $\boldsymbol p \cdot \nabla$ is a scalar, thus the force will point in the direction of $\boldsymbol E$, which is in the $\hat{r}$ direction, which is incorrect...

The presence of the derivatives can cause the direction to change, so you can't assume the force will point in the same direction as $\vec{E}$.

Since $\boldsymbol p = p \hat{\theta} = p_\theta$, then $p_r = p_\phi = 0$ and:$$\boldsymbol p \cdot \nabla = \frac{1}{r \sin \theta} \frac{\partial}{\partial \theta} (p \sin \theta) = \frac{p}{r \sin \theta} \frac{\partial}{\partial \theta} (\sin \theta).$$

Where did the $p\sin\theta$ come from? Also, your expression for the gradient in spherical coordinates appears to be wrong. What convention are you following — is $\theta$ the angle from the z-axis or is it supposed to be the azimuthal angle?

 

[ehild]

Better to use polar coordinates in plane.

$$\vec F= (\vec p \cdot \nabla) \vec E= p_r \frac{\partial \vec E}{\partial r}+p_{\theta}\frac{1}{r}\frac{\partial \vec E}{\partial \theta}$$

In the problem, $\vec E = E(r) \hat r$ and $\vec p = p \hat \theta$

You have to note that $\hat r$ depends on θ, and

$$\partial \hat r /{ \partial \theta} = \hat \theta$$

$$\vec F= (\vec p \cdot \nabla) \vec E= p\frac{1}{r}E(r) \frac{\partial \hat r}{\partial \theta}$$

ehild