Gibbs Phenomenon:The maxima get smaller,the minima get bigger

[mathmari]

Hey!

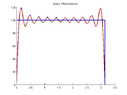
I am looking at the Gibbs Phenomenon for the function $\displaystyle{f(x)=sgn(x), x \in [-\pi, \pi]}$.

The Fourier series of this function is:

$$sgn(x) \sim s(x)=\sum_{k=1}^{\infty} \frac{4}{(2k-1) \pi} \sin{((2k-1)x)}$$

Since $f$ is odd, it's sufficient to look its behaviour at $[0, \pi]$.

$$s(x)=\frac{4}{\pi}[\sin{(x)}+\frac{\sin{(3x)}}{3}+\frac{\sin{(5x)}}{5}+ \dots]$$

$s(x)$ is even as for $x=\frac{\pi}{2}$, so it's sufficient to look at $[0, \frac{\pi}{2}]$.

$$s_{2n-1}(x)=\frac{4}{\pi}[\sin{(x)}+\frac{\sin{(3x)}}{3}+ \dots +\frac{\sin{((2n-1)x)}}{2n-1}]$$

After calculations, we have that
$$s_{2n-1}'(x)=\frac{2}{\pi} \frac{\sin{(2nx)}}{\sin{(x)}}$$
$$s_{2n-1}'(x)=0 \Rightarrow \sin{(2nx)}=0 \Rightarrow 2nx=m \pi \Rightarrow \\ x=\frac{m \pi}{2n}, m=1, \dots, 2n-1 \ \ \ \text{ : points of extrema }$$

$s_{2n-1}$ has $2n-1$ extrema at $(0, \pi]$

Going from $0$ to $\frac{\pi}{2}$ the maxima get smaller and the minima get bigger.

We can show that $\forall \delta: 0< \delta< \frac{\pi}{2}$, $s_{2n-1}(x)$ converges uniformly to $1$.Could you explain me the last two sentences?? (Wondering)

 

[Opalg]

Going from $0$ to $\frac{\pi}{2}$ the maxima get smaller and the minima get bigger.

View attachment 2678​

The Fourier series has a number of maxima, indicated by the blue dots in the picture, and a number of minima, indicated by the green dots. As $x$ goes from $0$ to $\pi/2$, the blue dots get lower and the green dots get higher. That is what is meant by the maxima getting smaller and the minima getting bigger.

We can show that $\forall \delta: 0< \delta< \frac{\pi}{2}$, $s_{2n-1}(x)$ converges uniformly to $1$.

As you increase the number of terms in the Fourier series, the first maximum (the highest blue dot) gets higher. When there are very many terms in the Fourier series, it will be about $1.18$. That is what constitutes the Gibbs phenomenon. But if you exclude that initial maximum by looking at the interval $[\delta,\pi/2]$ instead of the whole interval $[0,\pi/2]$, then on that slightly shorter interval the Fourier series converges uniformly to the constant function $1$ as the number of terms in the series increases.