Given surjective ##T:V\to W##, find isomorphism ##T|_U## of U onto W.

[zenterix]

Homework Statement

Axler, "Linear Algebra Done Right", Problem 8 Section 3D

Suppose $V$ is finite-dimensional and $T:V\to W$ is a surjective linear map of $V$ onto $W$. Prove that there is a subspace $U$ of $V$ such that $T|_U$ is an isomorphism of $U$ onto $W$. (Here $T|_U$ means the function $T$ restricted to $U$. In other words, $T|_U$ is the function whose domain is $U$ with $T|_U$ defined by $T|_U(u)=Tu$ for every $u\in U$.)

Relevant Equations

Since $T$ is surjective then $\text{range}(T)=W$.

I will use a proof by cases.

Case 1: dim V = dim W

Then $T=T|_V$ is an isomorphism of $V$ onto $W$. The reason for this is that it is possible to prove that if $T$ is surjective, which it is, then it is also injective and so it is invertible (hence an isomorphism).

Case 2: dim V < dim W

This case is impossible because a linear map to a larger dimensional space is not surjective.

Case 3: dim V > dim W

$$\text{dim} V = \text{dim null} T + \text{dim range} T = \text{dim null} T+\text{dim} W$$

Let $U$ be such that $V=U \bigoplus \text{null} T$, that is, the complement of $\text{null} T$.

Then

$$\text{dim} U + \text{dim null} T = \text{dim} V$$

$$\text{dim} U = \text{dim} W$$

$U$ and $W$ are isomorphic and $T|_U\in L(U,W)$ is an isomorphism because it is surjective

Pictorially, we have something like

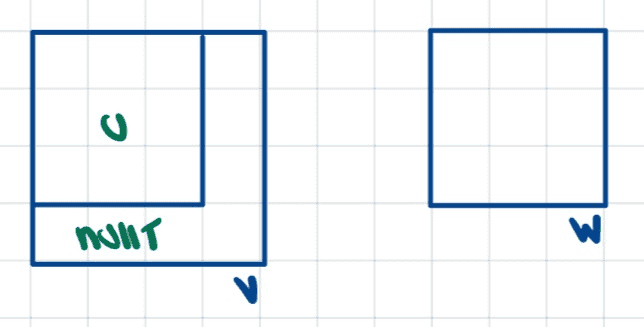
In each case, we can infer the desired result.

 

[nuuskur]

Yes, it suffices to consider any complement $U$ of $\mathrm{Ker}\,T$, i.e, $U\oplus \mathrm{Ker}\,T \cong V$. Then $T\vert _U :U\to W$ is automatically an isomorphism. To find $U$, it suffices to take any basis of $\mathrm{Ker}\,T$, extend it to a basis in $V$ and throw out the null part. In the special case of $\dim V=\dim W$, any basis of $\mathrm{Ker}\,T$ would have to be empty.