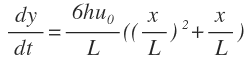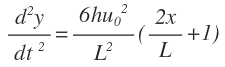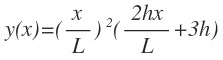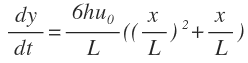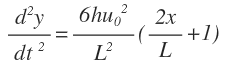How can I apply the chain rule correctly to functions?

[scook116]

I'm randomly having trouble applying the chain rule to functions (well, 1 function in particular), I was hoping someone could quickly walk me through this simple problem as I don't know where I've gone wrong. I've tried U substitution, chain/product rule, factoring answer...but I just can't see it

I'm trying to get View attachment 2119 from View attachment 2118

 

[MarkFL]

Okay, we are given:

$$\frac{dy}{dt}=\frac{6hu_0}{L}\left(\left(\frac{x}{L} \right)^2+\frac{x}{L} \right)$$

In order to obtain the result you cite via differentiation, it appears that we must assume:

$$x=t\,\therefore\,\frac{dx}{dt}=1$$

Now, the constant in front of the expression involving $x$ will simply be carried through:

$$\frac{d}{dt}\left(\frac{dy}{dt} \right)=\frac{6hu_0}{L} \frac{d}{dt}\left(\left(\frac{x}{L} \right)^2+\frac{x}{L} \right)$$

Now, can you differentiate term by term on the right, applying the power and chain rules?

 

[scook116]

I'm stuck on how the first expression has the numerator and denominator squared tho.

 

[MarkFL]

Ah, I did not notice $u_0$ being squared. Can you provide the original problem in its entirety?

 

[scook116]

Surely,
View attachment 2120 gives us the shape of the flight path, but say nothing about the speed of the airliner on that path. Begin by making the unrealistic assumption that horizontal speed is constant during the descent; that is dx/dt=u₀ use the chain rule int he form dy/dt=(dy/dx)(dx/dt) to show that vertical velocity of the airliner is View attachment 2121

then use the chain rule to show that the vertical acceleration d²y/dt² of the airliner along the flight path is View attachment 2122

 

[MarkFL]

Surely, View attachment 2120

also, dx/dt=u₀ and dy/dt=(dy/dx)(dx/dt). So sorry >.<

No worries...it just helps to have these details. So, let's begin with:

$$y=\left(\frac{x}{L} \right)^2\left(\frac{2hx}{L}+3h \right)$$

Differentiating with respect to $t$, we obtain:

$$\frac{dy}{dt}=2\left(\frac{x}{L} \right)\left(\frac{1}{L}\frac{dx}{dt} \right)\left(\frac{2hx}{L}+3h \right)+\left(\frac{x}{L} \right)^2\left(\frac{2h}{L}\frac{dx}{dt} \right)$$

Now factoring, we may write (using $$u_0=\frac{dx}{dt}$$):

$$\frac{dy}{dt}=\frac{2hu_0}{L}\left(\frac{x}{L} \left(\frac{2x}{L}+3 \right)+ \left(\frac{x}{L} \right)^2 \right)$$

$$\frac{dy}{dt}=\frac{6hu_0}{L}\left(\left(\frac{x}{L} \right)^2+\left(\frac{x}{L} \right) \right)$$

So, I do agree with the first derivative you posted. Now differentiate again, observing that $$u_0=\frac{dx}{dt}$$ is a constant:

$$\frac{d}{dt}\left(\frac{dy}{dt} \right)=\frac{6hu_0}{L} \frac{d}{dt}\left(\left(\frac{x}{L} \right)^2+\frac{x}{L} \right)$$

When you apply the rules of differentiation, you will get the result you cited. Can you give it a try seeing how I derived the first derivative?

 

[scook116]

I end up multiplying out many different expressions with what seems to be too crazy to be part of the solution. I am not sure if I'm picking U and V properly, and I think that might be throwing me in a loop. I end up with multiple expressions, one having 18hu₀x^2/L and it just doesn't seem like the right path.

I have OCD and focus on minute details especially when troubleshooting, I put myself into loops with almost every problem when I start thinking of the proper rules and methods.(Smoking)

 

[Deveno]

Let's concentrate on the expression:

$\dfrac{d}{dt}\left(\left(\dfrac{x}{L}\right)^2 + \dfrac{x}{L}\right)$

Linearity of the derivative gives us:

$\dfrac{d}{dt}\left(\left(\dfrac{x}{L}\right)^2 + \dfrac{x}{L}\right)$

$= \dfrac{d}{dt}\left(\left(\dfrac{x}{L}\right)^2 \right) + \dfrac{d}{dt}\left(\dfrac{x}{L}\right)$

Applying the chain rule to the first term gives:

$\dfrac{d}{dt}\left(\left(\dfrac{x}{L}\right)^2 \right) = 2\dfrac{x}{L} \cdot\dfrac{d}{dt}\left(\dfrac{x}{L}\right)$

At this point we have a common factor we can collect, so we have:

$\dfrac{d}{dt}\left(\left(\dfrac{x}{L}\right)^2 + \dfrac{x}{L}\right)$

$= \left(2\dfrac{x}{L} + 1\right)\cdot \dfrac{d}{dt}\left(\dfrac{x}{L}\right)$

Assuming $L$ is a constant, we can bring a factor of $\dfrac{1}{L}$ out front:

$= \dfrac{1}{L}\left(2\dfrac{x}{L} + 1\right)\cdot\dfrac{dx}{dt}$

Since we are given that $\dfrac{dx}{dt} = u_0$, we arrive at:

$\dfrac{d}{dt}\left(\left(\dfrac{x}{L}\right)^2 + \dfrac{x}{L}\right)$

$= \dfrac{u_0}{L}\left(2\dfrac{x}{L} + 1\right)$

and multiplying this by the constant factor:

$\dfrac{6hu_0}{L}$ gives us the "total answer":

$\dfrac{d^2y}{dt^2} = \dfrac{6hu_0^2}{L^2}\left(2\dfrac{x}{L} + 1\right)$

 

[scook116]

Guys, I'm not sure why I haven't been able to see these types of things, I see it now clear as hell but only after you two have helped me. This seems to happen often with me in calc. for example here when you took out "x/L"

At this point we have a common factor we can collect, so we have:

$\dfrac{d}{dt}\left(\left(\dfrac{x}{L}\right)^2 + \dfrac{x}{L}\right)$

$= \left(2\dfrac{x}{L} + 1\right)\cdot \dfrac{d}{dt}\left(\dfrac{x}{L}\right)$

I didnt see this at all.
Do you guys have ANY tips or tricks at all on how you do operations and or prioritize when doing calculus? I know all about 'go slow, don't miss anything'

 

[Deveno]

I didn't take out "x/L", I differentiated term-by-term, using the rule:

$(f + g)' = f' + g'$

Since we actually had $f = g^2$ using the chain rule gives us:

$(g^2 + g)' = 2g\cdot g' + g' = (2g + 1)g'$

(Here: $g(t) = \dfrac{x(t)}{L}$).

In general, when differentiating, it is often easier to separate sums first, before applying rules like the product rule or the chain rule, which tend to "expand" as you differentiate. Also, pulling out constant factors first, keeps what you are differentiating "as simple as possible".

"Combining like terms" often just takes a certain "knack" for recognizing "when is the right time to combine". Sometimes it's better to wait until later, sometimes it's better to do it as soon as you can, there's really no hard and fast rule.