- #1
roam
- 1,271
- 12
I am trying to write a very basic Matlab code to preform the split-step Fourier method on the nonlinear Schrodinger equation:
$$\frac{\partial A(z,T)}{\partial z} = -i \frac{\beta_2}{2} \frac{\partial^2A}{\partial T^2} + i \gamma |A|^2 A \ \ (1)$$
I want the program to make 3D plots of Gaussian input pulses (##A(0, T) = \sqrt{P_0} exp (-T^2/(2T_0^2))##) propagating over different distances. It should look something like this:
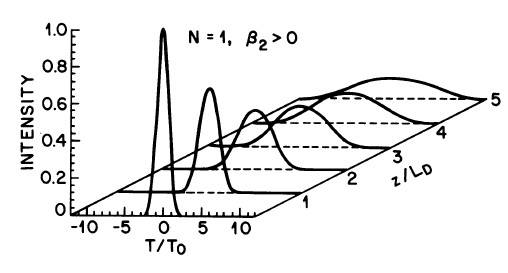
Attempt:
Here is my code (I chose some dummy values to check whether the code is working):
But the code doesn't work. There is no graph generated and I get the message that "Matrix dimensions must agree" I think because omega is a 1 by 15 row vector, and so is exp(v.*D), but v is a different size. How can I fix this?
Is the overall structure of the code correct or do we need to do this differently?
Any help would be greatly appreciated.
P.S.
The split-step Fourier method I am asked to use works by writing (1) as:
$$\frac{\partial A}{\partial z} = \left( \hat{D} + \hat{N} \right) A$$
With ##\hat{D} = -i (\beta_2 / 2) \partial^2 /\partial T^2## is the linear disperiosn operator while ##\hat{N} = i \gamma |A|^2## is the nonlinear operator. So for a step size ##h##, ##z \to z+h## we have
$$A(z,T) \to e^{h \hat{N}} A(z,t) \approx exp \Big[ ih \gamma |A(z,T)|^2 \Big] A(z,T).$$
$$\frac{\partial A(z,T)}{\partial z} = \hat{D} A(z,T)$$
becomes after temporal Fourier transform
$$\frac{\partial \tilde(A) (z, \Omega)}{\partial z} = \hat{D} (-i \Omega) \tilde{A} (z, \Omega)$$
an exact solution of which is ##e^{h \hat{D} (-i \Omega)} \tilde{A} (z, \Omega).##
Combining the two equations we get the following for a full integration step:
$$ \therefore \ A(z+h, T) = e^{h \hat{D}} e^{h \hat{N}} A(z,T) \approx FT^{-1} \Big[ e^{ih\beta_2 \Omega^2/2} FT [e^{ih \gamma |A(z,T)|^2} A(z,T)] \Big].$$
$$\frac{\partial A(z,T)}{\partial z} = -i \frac{\beta_2}{2} \frac{\partial^2A}{\partial T^2} + i \gamma |A|^2 A \ \ (1)$$
I want the program to make 3D plots of Gaussian input pulses (##A(0, T) = \sqrt{P_0} exp (-T^2/(2T_0^2))##) propagating over different distances. It should look something like this:
Attempt:
Here is my code (I chose some dummy values to check whether the code is working):
Code:
b=20; % in ps^2/km
s=b/2; % dispersive term
gamma = 2^(-10); % nonlinear term
h=1000; % propagation stepsize
N=100; % number of steps (Length traveled = h*N)
dt=2^(-10); % time step
P0=.00064; % input powr in watts
A0=sqrt(P0); % Amplitude
tau =- 4096e-12:1e-12: 4095e-12;
t0=125e-12; % input pulse width in seconds
omega=0.1:0.1:1.5;
u=A0*exp((-tau.^2)/(2*t0).^2); % Gaussian input pulse
%Plot input pulse
figure(1)
plot(abs(u),'b');
title('Input Pulse'); xlabel('Time'); ylabel('Amplitude');
for n = 1:N
%Solve nonlinear part (D=0)
u = u.*exp(i*h*gamma*abs(u).^2);
%Solve linear part in Fourier space (N=0)
v = fft(u);
D = i*s*omega.^2;
v = v.*exp(h.*D); % analytical soln
u = ifft(v); % back to real space
u = u.*exp(i*gamma*abs(u).^2*h);
end
%Plot results
figure(2);
w=waterfall(x,t,u')
set(w,'edgecolor','b');
title('Evolution of pulse shapes');
ylabel('distance (km)'), xlabel('Time (ps)'),zlabel('amplitude'); axis([-gridscale gridscale 0 tmax 0 zmax]), grid onBut the code doesn't work. There is no graph generated and I get the message that "Matrix dimensions must agree" I think because omega is a 1 by 15 row vector, and so is exp(v.*D), but v is a different size. How can I fix this?
Is the overall structure of the code correct or do we need to do this differently?
Any help would be greatly appreciated.
P.S.
The split-step Fourier method I am asked to use works by writing (1) as:
$$\frac{\partial A}{\partial z} = \left( \hat{D} + \hat{N} \right) A$$
With ##\hat{D} = -i (\beta_2 / 2) \partial^2 /\partial T^2## is the linear disperiosn operator while ##\hat{N} = i \gamma |A|^2## is the nonlinear operator. So for a step size ##h##, ##z \to z+h## we have
$$A(z,T) \to e^{h \hat{N}} A(z,t) \approx exp \Big[ ih \gamma |A(z,T)|^2 \Big] A(z,T).$$
$$\frac{\partial A(z,T)}{\partial z} = \hat{D} A(z,T)$$
becomes after temporal Fourier transform
$$\frac{\partial \tilde(A) (z, \Omega)}{\partial z} = \hat{D} (-i \Omega) \tilde{A} (z, \Omega)$$
an exact solution of which is ##e^{h \hat{D} (-i \Omega)} \tilde{A} (z, \Omega).##
Combining the two equations we get the following for a full integration step:
$$ \therefore \ A(z+h, T) = e^{h \hat{D}} e^{h \hat{N}} A(z,T) \approx FT^{-1} \Big[ e^{ih\beta_2 \Omega^2/2} FT [e^{ih \gamma |A(z,T)|^2} A(z,T)] \Big].$$