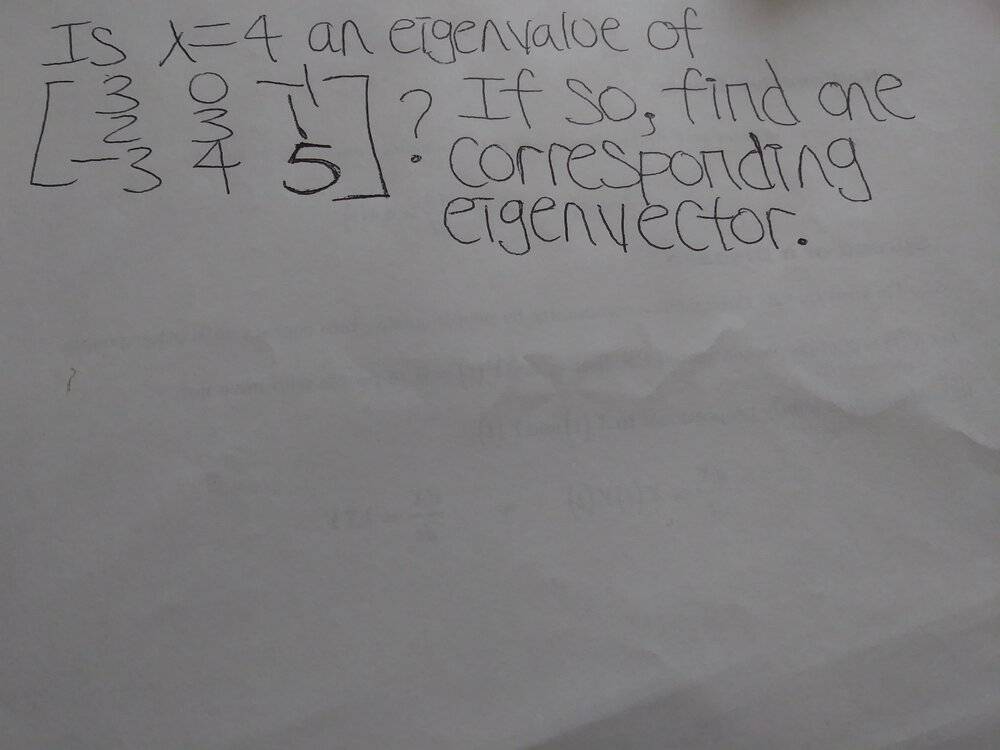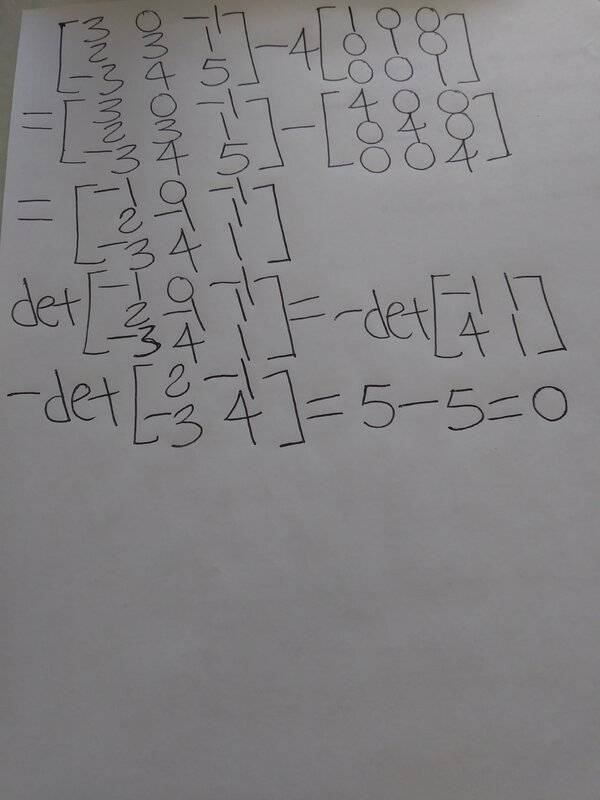- #1
Math100
- 756
- 201
- Homework Statement
- Is lambda=4 an eigenvalue of the given matrix? If so, find one corresponding eigenvector.
- Relevant Equations
- None.
The determinant is 0, which means that A-4I has a nullspace, and there is an eigenvector with eigenvalue 4. In the textbook, the answer says "Yes, [1, 1, -1]" for this problem. But I don't know how to find the corresponding eigenvector for this problem. Below is my work.