How to know which way to integrate?

[Rijad Hadzic]

Homework Statement

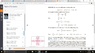
Please see the attachment. This isn't a question, but more so my understanding of the book.

Please read the middle paragraph. So I'm suppose to take an integral of cos(x)sin(x)

Wolfram and my book give the answer as -(1/2)cos(x)^2, but when I did it I got it as (1/2)sin(x)^2.

Homework Equations

The Attempt at a Solution

Taking the derivative of (1/2)sin(x)^2. you do indeed get cos(x)sin(x). But when evaluating the differential equation for the initial condition, when using (1/2)sin(x)^2. you get c = 4, but when using -(1/2)cos(x)^2 you get 3.

How am I suppose to know which one to use? Taking the derivative of both you get the same answer, but when doing the initial condition you don't..

 

[Rijad Hadzic]

I just don't see the point in making the integral -\int {cos(x)-(sin(x)dx) } when you can just do \int {sin(x)(cos(x)dx) } with u = sinx du = cosx dx ... and obviously it gives different answers in the end so yeah.. does anyone know why exactly?

Now that I look back on it... so I get 4 for my constant value... so what?! My answer could still be right then, right?

So if I have y^2(1-x^2) + (sin(x))^2 = 4, it should be the same as y^2(1-x^2) - (cos(x))^2 = 3

 

[ehild]

I just don't see the point in making the integral -\int {cos(x)-(sin(x)dx) } when you can just do \int {sin(x)(cos(x)dx) } with u = sinx du = cosx dx ... and obviously it gives different answers in the end so yeah.. does anyone know why exactly?

You forgot the integration constant.
$\int{\cos(x) \sin(x)dx}=\frac{1}{2}\sin^2(x) + C_1$ and it is the same as $-\frac{1}{2}\cos^2(x) + C_2$ , as
$\sin^2(x)+\cos^2(x)=1$.
So $\frac{1}{2}\sin^2(x) + C_1 =-\frac{1}{2}\cos^2(x)+\frac{1}{2}+C_1$, so
$C_2=0.5+C_1$

 

[Rijad Hadzic]

Gotcha. Thanks for that breakdown there. Really puts the relationship between sin/cos in a way that I can understand. Thanks.