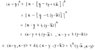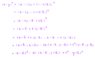- #1
Onezimo Cardoso
- 11
- 2
Homework Statement
Let ##C \subset \mathbb{R}^n## a convex set. If ##x \in \mathbb{R}^n## and ##\overline{x} \in C## are points that satisfy ##|x-\overline{x}|=d(x,C)##, proves that ##\langle x-\overline{x},y-\overline{x} \rangle \leq 0## for all ##y \in C##.
Homework Equations
By definition we have ##d(x,C) = inf \{ |x-z| ; z \in C \}##.
And if ##C## is a convex set, then for any two points ##v,w \in C## we have ##(1-t)v+tw \in C##.
The Attempt at a Solution
Due the fact that ##|x-\overline{x}|=d(x,C)## , I know that ##|x-\overline{x}|^2 \leq |x-z|^2## for all ##z \in C##.
I tried to sketch a prove by contraction. So I supposed that there is an ##y \in C## that ##\langle x-\overline{x},y-\overline{x} \rangle > 0##.
Then I used the fact that ##C## is a convex set, so ##z=(1-t)y+t\overline{x} \in C##, where ##t \in [0,1]##.
Then I intend to conclude something like ##|x-z|^2 < |x-\overline{x}|^2##, what would be an absurd:
But the fact is I came nowhere with my attempt... =(