Integrating F over a Paraboloid Region

[lumpyduster]

Homework Statement

Let F = <x, z, xz> evaluate ∫∫F⋅dS for the following region:

x²+y²≤z≤1 and x≥0

Homework Equations

Gauss Theorem

∫∫∫(∇⋅F)dV = ∫∫F⋅dS

The Attempt at a Solution

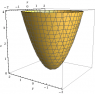
This is the graph of the entire function:

Thank you Wolfram Alpha.

But my surface is just the half of this paraboloid where x is positive. So I thought if I looked down the x-axis I would get something like this:

But only the right half of the circle (from -3π/2 to π/2)...

The integral I set up is the following:

∫∫∫xdzdxdy (x is the dot product of ∇ and F)

I converted to polar coordinates

∫∫∫r²cosθdzdrdθ

Bounds:
r²≤z≤1

0≤r≤1

-3π/2≤θ≤π/2

I ended up getting

-(4/15)∫cosθdθ
-3π/2≤θ≤π/2

(4/15)[sin(π/2)-sin(-3π/2)] = 0

Answer should be 4/15 according to the back of the book.

 

[LCKurtz]

Homework Statement

Let F = <x, z, xz> evaluate ∫∫F⋅dS for the following region:

x²+y²≤z≤1 and x≥0

Homework Equations

Gauss Theorem

∫∫∫(∇⋅F)dV = ∫∫F⋅dS

The Attempt at a Solution

But only the right half of the circle (from -3π/2 to π/2)...

That is not the correct range for the $x$ positive half of the circle. Do you really mean $-\frac{3\pi}{2}$?

The integral I set up is the following:

∫∫∫xdzdxdy (x is the dot product of ∇ and F)

Check $\nabla \cdot \vec F$ again.

 

[haruspex]

This is the graph of the entire function

Well, no, it shows the region (at least, it would if truncated at z = 1 instead of z = 4).

x is the dot product of ∇ and F

Are you sure? I get another term.

-3π/2≤θ≤π/2

Think about that lower bound again. Where is -3π/2 in the plane?

Edit: beaten to the post by LCK (again).

 

[lumpyduster]

That is not the correct range for the $x$ positive half of the circle. Do you really mean $-\frac{3\pi}{2}$?



Check $\nabla \cdot \vec F$ again.

Well, no, it shows the region (at least, it would if truncated at z = 1 instead of z = 4).

Are you sure? I get another term.

Think about that lower bound again. Where is -3π/2 in the plane?

Edit: beaten to the post by LCK (again).

Not sure at all about the lower bound... Should it be 3π/2? I was going to also say 0 to π, but if my upper bound is correct then that would be wrong.

 

[haruspex]

Not sure at all about the lower bound... Should it be 3π/2?

That should work.

 

[lumpyduster]

That should work.

So I will integrate from π/2 to 3π/2? I guess I'm confused how to take into account that x≥0 when switching to polar coordinates. I just know I want to go from x=0 to x=1 on the Cartesian coordinate system. Would 0 to π also work?

 

[haruspex]

So I will integrate from π/2 to 3π/2?

No, you said 3π/2 for the lower bound, not the upper bound.

 

[lumpyduster]

No, you said 3π/2 for the lower bound, not the upper bound.

Yeah I probably sound like a total noob here, but I've never done an integral where my lower bound was greater than my upper bound... Will try and report back if necessary :)

 

[haruspex]

Yeah I probably sound like a total noob here, but I've never done an integral where my lower bound was greater than my upper bound... Will try and report back if necessary :)

You can take the lower bound to be -π/2 if you prefer. It should give the same result.

 

[lumpyduster]

You can take the lower bound to be -π/2 if you prefer. It should give the same result.

I just don't know how to get these bounds though... Can I say that since 0≤x≤1 and since x=rcosθ and r=1, that arccos(0)≤θ≤arccos1?

Thank you for your help!

 

[haruspex]

I just don't know how to get these bounds though... Can I say that since 0≤x≤1 and since x=rcosθ and r=1, that arccos(0)≤θ≤arccos1?

Yes, but that doesn't pin down the bounds on theta. For example, π/2 to 0 would seem to be right if you base it only that. I don't think you can do better than consider what the physical region looks like and deduce the range for theta from that. Just bear in mind that running theta continuously from the lower bound to the upper bound (together with the ranges on r and z) must reach each point of the region exactly once, and no points outside the region.

 

[LCKurtz]

Yes, but that doesn't pin down the bounds on theta. For example, π/2 to 0 would seem to be right if you base it only that. I don't think you can do better than consider what the physical region looks like and deduce the range for theta from that. Just bear in mind that running theta continuously from the lower bound to the upper bound (together with the ranges on r and z) must reach each point of the region exactly once, and no points outside the region.

Sorry to be so late getting back to this thread, but I think something is getting missing in translation. Usually in describing limits on an integral when you say from $a$ to $b$ you would assume $a$ is the lower limit and $b$ is the upper limit, and $a < b$. You integrate in the positive direction. So you would say from $0$ to $\pi / 2$ to describe the first quadrant, not $\pi /2$ to $0$. If you want to describe the right side of the circle you could go from $-\pi /2$ to $\pi /2$ or from $3\pi /2$ to $5\pi /2$ or something similar.

 

[haruspex]

Sorry to be so late getting back to this thread, but I think something is getting missing in translation. Usually in describing limits on an integral when you say from $a$ to $b$ you would assume $a$ is the lower limit and $b$ is the upper limit, and $a < b$. You integrate in the positive direction. So you would say from $0$ to $\pi / 2$ to describe the first quadrant, not $\pi /2$ to $0$. If you want to describe the right side of the circle you could go from $-\pi /2$ to $\pi /2$ or from $3\pi /2$ to $5\pi /2$ or something similar.

I think you misunderstand the point I was making. I was saying that in order to find the limits on theta for integration it is not sufficient to consider the range of values that cos(theta) can take. You might miss part of the range (since over the range of theta some cos(theta) values are repeated), or include regions which are not in the range (like going from 0 to 5pi/2), or, as you note, get the upper and lower limits reversed.