Irodov problem 1.12 — A 3-body gravitational attraction problem

[John10086]

Homework Statement

Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?

Relevant Equations

vt = s

The thing is, I've already looked up at the solution online at it's t= 2a/3v. But I've approached it a different way and I can't really tell what I'm doing wrong, my solutions gives out t= (a/√3v )* (π/3),I don't know what's wrong with it. Here's my approach:

The points will meet at the centroid of the triangle, at distance l= a/√3 from the points, and their trajectory will be curved.
Argument 1: Since the modulus of the velocities isn't changing but the direction is, there must be a centripetal acceleration and the trajectory is a segment of a circle of radius r. Therefore acceleration (and position vector from the center of the circumference) must be perpendicular to v.

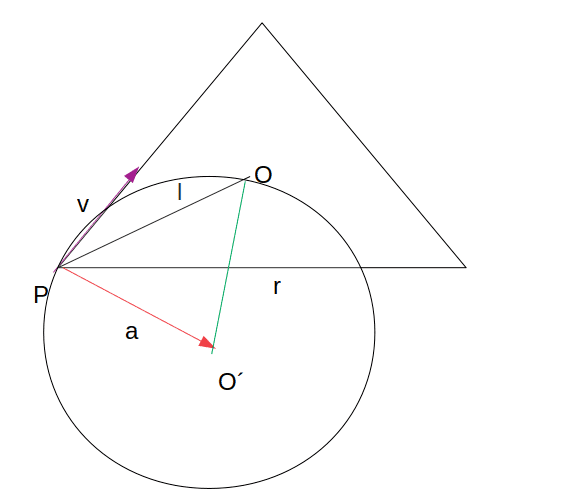
By using the fact its an equilateral triangle, we find that POO' is an equilateral triangle as well therefore r=l. Distance traveled by the point is (π/3)*r.
vt=(π/3)*r.
t= (π/3v)*r.
t= (a/√3v )* (π/3)

Please help, I have no idea what's wrong with my approach. Thanks

 

[haruspex]

Since the modulus of the velocities isn't changing but the direction is, there must be a centripetal acceleration and the trajectory is a segment of a circle

Only if the centripetal acceleration is constant.

 

[John10086]

Only if the centripetal acceleration is constant.

Thanks, for the feedback. That makes a lot of sense, but how can I know for sure the centripetal acceleration isn't constant?

 

[Charles Link]

Try computing $\frac{d \phi}{ds}=\frac{1}{r}$ where $r$ is the instantaneous radius of curvature, and you will see it is not constant. If it were, the problem would be fairly simple.
The best I can tell, this one is a spiral, but I haven't solved it yet.
I computed the above by taking the instantaneous length $l$ of the side of the triangle, (the scenario is always an equilateral triangle that will be rotating and shrinking), and computing the $\Delta \phi$ that results from a $\Delta s$. The result I got is that $\frac{\Delta \phi}{\Delta s}$ is inversely proportional to $l$.
Note: $\phi$ is the angle (w.r.t. the horizontal) of the velocity vector of a given vertex.

 

[haruspex]

The best I can tell, this one is a spiral, but I haven't solved it yet.

The easy way to solve such problems is by considering relative velocity along the line joining one to the next.
It's not made clear, but I am guessing the solution @John10086 found online gives the method as well as the answer.

but how can I know for sure the centripetal acceleration isn't constant?

The point, surely, is that you have not shown that it is.

 

[Charles Link]

I just solved it now. It is kind of simple in a way=you don't need to compute the trajectory. Instead, similarly to computing $\frac{\Delta \phi}{\Delta s}$, you compute $\frac{\Delta r}{\Delta s}$ for the instantaneous triangular case. It's simple trigonometry. The integrated $\Delta r$ is just the length of the vertex to the centroid. The integrated $\Delta s$ follows immediately. $\\$ The trajectory is not a circle=I was able to show that with the $\frac{\Delta \phi}{\Delta s}$ computation, but any solution computing an arc length of the path by using the exact trajectory is likely to be very difficult.

 

[John10086]

Thanks a lot guys, and yes I did see the solution online using relative velocity along the line, It's just that I couldn't figure out why my solution was wrong. I have more clarity now, I'll be more careful next time when assuming things!

 

[Charles Link]

It was a good guess, although incorrect, to think it might be a circular path. I think the computation of the exact path on this one might prove very difficult. [Edit: See post 11 for the exact path.] I was able to show the acceleration would be position dependent, and the form was not simple.
For a problem where the centripetal acceleration increases linearly with time see https://www.physicsforums.com/insights/frenet-equations-2-d-result-cornu-spiral/

 

[John10086]

Woah, thanks for the link, I was just wondering how that'd look like

 

[archaic]

You can consider $a^2(t+dt)=(v\,dt)^2+(a(t)-v\,dt)^2-2(v\,dt)(a(t)-v\,dt)\cos(\frac{\pi}{3})$ (cosine rule) and try to find the rate of change of $a(t)$ using the formal definition of a derivative.
$$\begin{align*}
a^2(t+dt)&=(v\,dt)^2+(a(t)-v\,dt)^2-2(v\,dt)(a(t)-v\,dt)\cos(\frac{\pi}{3})\\
&=(v\,dt)^2+a^2(t)-2a(t)(v\,dt)+(v\,dt)^2-a(t)(v\,dt)+(v\,dt)^2\\
&=a^2(t)-3a(t)(v\,dt)+3(v\,dt)^2
\end{align*}$$
Bring the $a^2(t)$ to the other side and remove infinitesimals of higher orders:
$$\begin{align*}
a^2(t+dt)-a^2(t)=-3a(t)(v\,dt)&\Leftrightarrow\frac{a^2(t+dt)-a^2(t)}{dt}=-3va(t)\\
&\Leftrightarrow 2a(t)a'(t)=-3va(t)\\
&\Leftrightarrow a'(t)=-\frac{3v}{2}
\end{align*}$$
The side length is decreasing with $da=-(3/2)v\,dt$ each $dt$, so, if you sum all the decrements, you will obtain the negative of the length, or:
$$a=-\int_0^{t_f}a'(t)dt=\int_0^{t_f}\frac{3v}{2}dt=\frac{3v}{2}t_f\Leftrightarrow t_f=\frac{2a}{3v}$$

 

[Charles Link]

Item of interest:
See https://en.wikipedia.org/wiki/Logarithmic_spiral
If I interpreted my calculations correctly, the differential equation for this one is of the form $\frac{d \theta}{dr}=\frac{C}{r}$, and this one could be solved as a logarithmic spiral, but the solution we have above is sufficient.
Note: With our solution above, we get a result that $r=R_o-cs$, so that this $\frac{d \theta}{dr }$ result follows from the $\frac{d \phi}{ds}$ result.

 

[archaic]

You can consider $a^2(t+dt)=(v\,dt)^2+(a(t)-v\,dt)^2-2(v\,dt)(a(t)-v\,dt)\cos(\frac{\pi}{3})$ (cosine rule) and try to find the rate of change of $a(t)$ using the formal definition of a derivative.

I would like to add:
The angle in the cosine is constant since the particles will move towards each other by the same amount and in the same way in an infinitesimal time, i.e the triangle they form is always equilateral.

 

[Charles Link]

I would like to add:
The angle in the cosine is constant since the particles will move towards each other by the same amount and in the same way in an infinitesimal time, i.e the triangle they form is always equilateral.

The diagram you posted was good. This is a similar approach that I used, and you can make a polar coordinate system $(r, \theta)$, with the origin being the centroid of the triangle. (By symmetry, that is ultimately where the vertices converge). Alternatively, you can compute $dr/dt$ from the vector $\vec{v}$,and then get the answer for the time. $\\$ For some extra work, you can compute $dr/d \theta$, and then get $r$ as a function of $\theta$. See post 11.

 

[archaic]

For some extra work, you can compute $dr/d \theta$, and then get $r$ as a function of $\theta$. See post 11.

Someone here had the same reasoning also:
https://math.stackexchange.com/a/3296473/630728

 

[kuruman]

Note that the velocity is always directed along the side of an equilateral triangle that rotates while it shrinks. Since the speed $v$ is constant, the radial velocity is also constant, $v_r=v\cos(30^o)$. Thus, the total time is given by $t=\dfrac{h}{v_r}$ where $h$ is the distance from the apex to the center of the equilateral triangle. This works, of course, with any $N$-sided regular polygon; it's just the angle that differs, and the general expression can be easily derived.