Lagrangian of a sphere rolling down a moving incline

[kafn8]

Homework Statement

A sphere of mass m2 and radius R rolls down a perfectly rough wedge of mass m1. The wedge sits on a frictionless surface so as the sphere rolls down, the wedge moves in opposite direction. Obtain the Lagrangian.

Homework Equations

The Attempt at a Solution

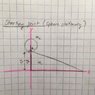
Here's my diagram of the situation. I used a cartesian system with the origin at the bottom corner of the wedge. Also I treated the sphere as the point in contact with the wedge, and I treat the wedge as a point at its top corner.

I imagined that as the sphere rolls down the incline, its y-value changes but the x-value stays the same as the wedge slips to the left (similar to someone slipping on a banana peel, or running on a free-floating log). Also, in an attempt to have x and y as my generalized coordinates, I expressed the distance s the sphere makes along the incline in terms of x and y (see pic)

My Lagrangian worked out to be the following:

The problem I have with this is that if I were to continue finding equations of motion from this Lagrangian, I'd clearly have no equations to express the acceleration in the x-direction. I'm left with only acceleration in the y-direction but the wedge is clearly moving away from the origin so there should be x-acceleration there.

Should I be using a different point of origin? Or maybe a different coordinate system altogether??

 

[BvU]

Hello kafn8,

but the x-value stays the same

Ah, so there is some horizontal force at work as well ? Because if the sphere x remains the same, the center of mass of the whole system moves sideways !

PS how many degrees of freedom do you have ? So how many generalized coordinates do you really need ?

$y_1$ is a funny choice. What does it tell you ? And: what is $\dot y_1$ ?

 

[kafn8]

Hello kafn8,

Ah, so there is some horizontal force at work as well ? Because if the sphere x remains the same, the center of mass of the whole system moves sideways !

PS how many degrees of freedom do you have ? So how many generalized coordinates do you really need ?

$y_1$ is a funny choice. What does it tell you ? And: what is $\dot y_1$ ?

Thanks, BvU.

The wedge is moving in one dimension but the sphere's position can be expressed by x and y coordinates. That's where I get confused. Should I consider the motion of the wedge as my limiting factor and just call it one degree of freedom?

I think I was just forcing the problem to have x and y coordinates - the toughest part of these problems is figuring out an appropriate coordinate system and I saw some potential in the cartesian system. $y_1$ and $\dot y_1$ don't make sense. It describes the top point of the wedge as having some vertical motion relative to the surface, and that's clearly not happening. $y_1$ is a constant.

 

[BvU]

A way to look at it is: you have a lot of coordinates but also a lot of constraints (wedge moves horizontally only, sphere moves on wedge surface,rolling without slipping). The Lagrange multipliers will tell you the forces of the constraints, which you may or may not be interested in. Pick enough generalized coordinates but no more than necessary. An there is no horizontal force on the whole system, so the center of mass stays in place...