Light clocks measure conformal time - detailed argument

[jcap]

Let us assume that an observer is stationary at the origin in expanding space. We assume the FRW metric near the origin is given by:
$$ds^2=-dt^2+a(t)^2dr^2$$
Let us assume that the observer measures time by bouncing a light beam at a mirror that is at a constant proper unit distance away from him.

By substituting $dt=0$ in the metric we find that an interval of proper distance $ds$ is given by:
$$ds=a(t)\ dr$$
Integrating we find the proper distance $S$ to an object at co-moving co-ordinate $r$ is given by:
$$S=a(t)\ r$$
Thus if the mirror has constant proper distance $S=1$ then it follows a path in co-moving co-ordinates given by:
$$r=\frac{1}{a(t)}$$
A light beam is described by substituting $ds=0$ in the metric to get the null geodesic:
$$dr=\frac{dt}{a(t)}$$
Integrating we get the path of a light beam:
$$r = \int \frac{dt}{a(t)}$$
The spacetime diagram below shows the observer attempting to measure cosmological time $t$ using the light clock.

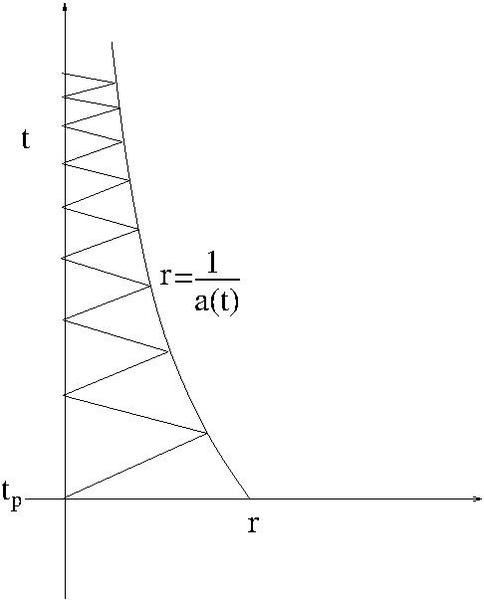
One can see that as the mirror gets closer in co-moving co-ordinate $r$ the period of the light clock gets smaller and smaller. Thus the light clock is getting faster relative to cosmological time $t$.

Now let us make a transformation to conformal time $\tau$ given by the relationship:
$$d\tau=\frac{dt}{a(t)}$$
The transformed radial co-ordinate $\rho$ is given by:
$$\rho\ d\tau = r\ dt$$
Therefore the path of the mirror in conformal co-ordinates is given by:
$$\rho = r\ \frac{dt}{d\tau}$$
$$\rho = \frac{1}{a(t)} \cdot a(t) = 1$$
The path of a light beam in co-moving co-ordinates is given by:
$$dr=\frac{dt}{a(t)}$$
Therefore in conformal co-ordinates we have:
$$d\rho=d\tau$$
On integrating:
$$\rho = \tau$$
Thus in conformal co-ordinates the light clock is described by the diagram below:

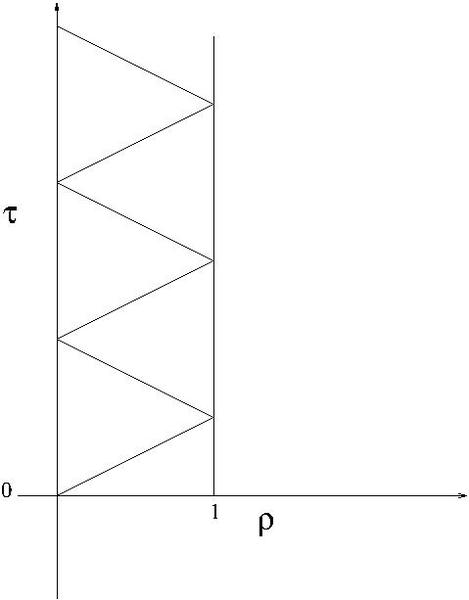
One can now see that the light clock period is constant - the clock is working properly.

Thus a light clock measures conformal time $\tau$ rather than cosmological time $t$.

Is this argument correct?

 

[Chalnoth]

That's a somewhat odd clock to use. Why would you use a clock whose length scale changes with the expansion? The use of such a clock would, for example, result in atoms having different spectral lines over time as a result of the expansion.

 

[jcap]

I assume that the proper length of the clock stays constant.

If atomic time is conformal time then one would expect the spectral lines of atoms to increase with cosmological time. This would be an alternative explanation of the cosmological redshift (assuming that photon energies actually stay constant as the Universe expands).

 

[Chalnoth]

I assume that the proper length of the clock stays constant.

What you've written assumes that the co-moving length stays constant, which is a different thing than the proper length.

If atomic time is conformal time then one would expect the spectral lines of atoms to increase with cosmological time. This would be an alternative explanation of the cosmological redshift (assuming that photon energies actually stay constant as the Universe expands).

This sort of picture would have chemistry behave differently at different times based upon the expansion of the universe far away. It would be extraordinarily cumbersome and unhelpful to work in these coordinates for any sort of small-scale system. It is sometimes useful to use co-moving distance and conformal time (this is the time coordinate you're using above) for cosmological measurements. But these aren't proper distance or time, and aren't useful for anything small-scale (that is, they make the math more complex because they add new unnecessary parameters).

 

[jcap]

What you've written assumes that the co-moving length stays constant, which is a different thing than the proper length.

In my argument I start off by assuming that the proper distance to the mirror is constant ($S=1$) which implies that the co-moving distance in terms of cosmological time, $r(t)$, is given by:
$$r(t)=\frac{1}{a(t)}$$
It is only when I additionally change the time variable from cosmological time $t$ to conformal time $\tau$ in the expression above that I derive a constant co-moving distance in terms of conformal time, $r(\tau)$, given by:
$$r(\tau)=1$$
Thus when one transforms to conformal time both the proper distance and the co-moving distance to the mirror are constant. (I think that's true - I might be wrong!)

 

[Chalnoth]

In my argument I start off by assuming that the proper distance to the mirror is constant ($S=1$) which implies that the co-moving distance in terms of cosmological time, $r(t)$, is given by:
$$r(t)=\frac{1}{a(t)}$$
It is only when I additionally change the time variable from cosmological time $t$ to conformal time $\tau$ in the expression above that I derive a constant co-moving distance in terms of conformal time, $r(\tau)$, given by:
$$r(\tau)=1$$
Thus when one transforms to conformal time both the proper distance and the co-moving distance to the mirror are constant. (I think that's true - I might be wrong!)

That's not possible. The proper distance is independent of the choice of time coordinate.

 

[Jorrie]

Thus when one transforms to conformal time both the proper distance and the co-moving distance to the mirror are constant. (I think that's true - I might be wrong!)

This 'three-panel diagram' by Tamara Davis gives some graphic insights into the relationships between cosmic distances and times.
(http://arxiv.org/abs/astro-ph/0310808 figure 1)

 

[PeterDonis]

One can see that as the mirror gets closer in co-moving co-ordinate $r$ the period of the light clock gets smaller and smaller.

This is obviously wrong; if the proper distance is constant the round-trip light travel time must be constant. If you're not getting that result, then you're modeling something incorrectly. I suspect the error is in how you're translating the assumption of constant proper distance into math.

 

[PeterDonis]

Integrating we get the path of a light beam:

​

$$
r = \int \frac{dt}{a(t)}
$$

I'm also confused as to how you can evaluate this integral and produce your chart without knowing the functional form of $a(t)$.

 

[PeterDonis]

The transformed radial co-ordinate $\rho$

The transformation to conformal time does not change any other coordinates; it only changes the time coordinate. What you are doing is not a transformation to conformal coordinates; it's a transformation to what one might call "proper distance coordinates", where the radial coordinate $\rho$ directly represents proper distance in the radial direction (the radial coordinate in conformal coordinates doesn't do that). That's why you obtained $\rho = 1$ for the mirror.

(I'm actually not sure you've done the transformation correctly; but if you have, it's not a transformation to conformal coordinates.)

 

[jcap]

I can now see that my transformation to $\rho$ was wrong. I'm not changing variables under an integral sign so I shouldn't use $\rho(\tau)=r(t)dt/d\tau$. I still think my argument about constant proper distance is ok. If proper distance is constant then $r \propto 1/a(t)$. In co-moving cordinates the mirror is getting closer even though the proper distance is constant. Maybe I'm wrong here as well - seems counter-intuitive.

I haven't worked out the paths of the light beams properly either.

Basically starting with some valid assumption for $a(t)$ I need to derive the operation of the lightclock in detail using just the $t$,$r$ diagram.

 

[PeterDonis]

If proper distance is constant then $r \propto 1/a(t)$. In co-moving cordinates the mirror is getting closer even though the proper distance is constant.

This part is correct. The part that still needs working out, as you say, is the paths of the light beams in comoving coordinates, to show that the light travel time is constant (since the proper distance is constant).

 

[jcap]

I now realize that my idea is wrong.

The co-moving distance light travels in a small interval of cosmological time $\delta t$ is:
$$r = \frac{c \delta t}{a(t)}$$.
As we have $r \propto 1/a(t)$ then we get:
$$\frac{c \delta t}{a(t)} \propto \frac{1}{a(t)}$$
$$\delta t \propto 1$$
Therefore the light clock does measure cosmological time correctly.