- #1
Karl Karlsson
- 104
- 12
- Homework Statement
- Let ##V = \mathbb{C}([0, 1], \mathbb{C})## be the vector space of continuous functions ##f: [0,1] \rightarrow \mathbb{C}## with inner product:
$$\langle f|g \rangle = \int_0^1 \overline {f(t)}g(t)\;\mathrm{d}t$$
For ##h \in V## , let ##L_h: V \rightarrow V## be the operator defined by ##L_h(f)(t)=h(t)f(t)##.
b) Determine the adjoint operator to ##L_h##
c) For which functions is the operator ##L_h## self adjoint?
d) For which functions is the operator ##L_h## unitary?
e) Give example of one function h(t) such that the operator ##L_h## is self adjoint and has at least two different eigenvalues
- Relevant Equations
- $$\langle f|g \rangle = \int_0^1 \overline {f(t)}g(t)\;\mathrm{d}t$$
##L_h(f)(t)=h(t)f(t)##
b)
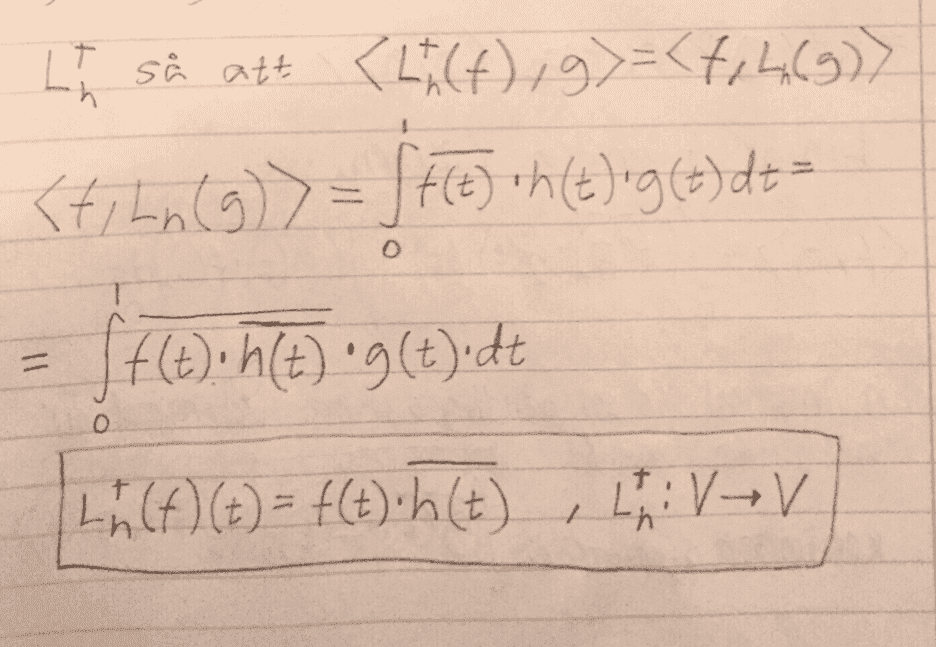
c and d):
In c) I say that ##L_h## is only self adjoint if the imaginary part of h is 0, is this correct?

e) Here I could only come up with eigenvalues when h is some constant say C, then C is an eigenvalue. But I' can't find tw therwise does b-d above look correct?
therwise does b-d above look correct?
Thanks in advance!
c and d):
In c) I say that ##L_h## is only self adjoint if the imaginary part of h is 0, is this correct?
e) Here I could only come up with eigenvalues when h is some constant say C, then C is an eigenvalue. But I' can't find tw
Thanks in advance!