Linear operator in 2x2 complex vector space

[jolly_math]

Homework Statement

see question below

Relevant Equations

basis

Let C^2x2 be the complex vector space of 2x2 matrices with complex entries. Let

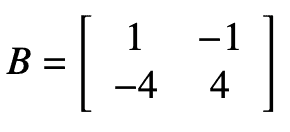and let T be the linear operator onC^2x2 defined by T(A) = BA. What is the rank of T? Can you describe T²?
____________________________________________________________

An ordered basis for C^2x2 is:

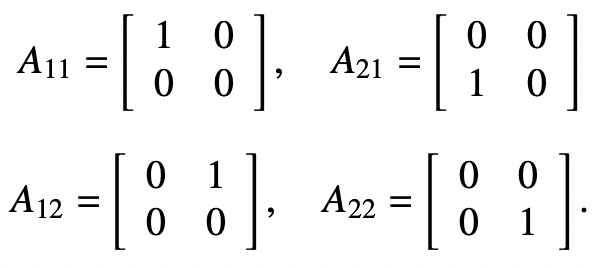
I don't understand the following statement:
If we identify C^2x2 with C⁴, then since

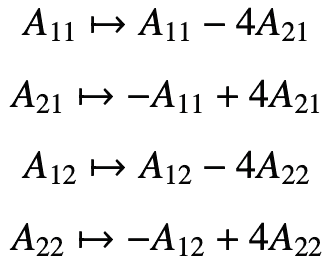, the matrix of the transformation is

.

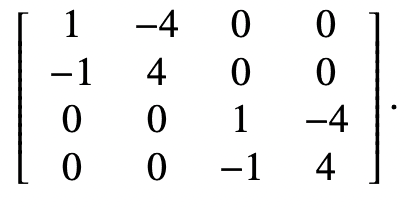Could anyone explain this? Thank you.

 

[Office_Shredder]

Do you know how to compute $T(A_{11})$?

 

[vela]

Could anyone explain this?

Which part specifically?

I think the 4x4 matrix should actually be the transpose of what you posted, but I might be missing something.

 

[Orodruin]

I think the 4x4 matrix should actually be the transpose of what you posted, but I might be missing something.

This depends on if we consider representing the $\mathbb C^4$ space as row or column vectors and is therefore up to convention. Without knowing the convention used we cannot say if it should be transposed or not.

What should be clear is that the operator $B$ acts separately on each column of $A$ and therefore can be decomposed into its separate action on $\mathbb C^2\oplus \mathbb C^2$ as $T(A) = T(a_1\oplus a_2)= (B a_1)\oplus(Ba_2)$. The question therefore can be handled by considering the rank of $B$ when acting on $\mathbb C^2$.

 

[jolly_math]

Do you know how to compute $T(A_{11})$?

No, I don't. I mainly don't understand how

was created, and why this results in

- I think there is more specific mathematical reasoning used that I can't see here. Thanks.

 

[Orodruin]

No, I don't. I mainly don't understand how View attachment 315063 was created, and why this results in View attachment 315064 - I think there is more specific mathematical reasoning used that I can't see here. Thanks.

If $T(A) = BA$, what is $T(A_{11})$? (Explicitly for the given $A_{11}$ and $B$)

 

[jolly_math]

If $T(A) = BA$, what is $T(A_{11})$? (Explicitly for the given $A_{11}$ and $B$)

$$
\begin{bmatrix}
1 & 0 \\
-4 & 0 \\
\end{bmatrix}
$$. I think I understand how

was created now. How does this lead to

? Thanks.

 

[Orodruin]

What matrix do you need to multiply the vector
$$
\begin{pmatrix} A_{11} \\ A_{21} \\ A_{12} \\ A_{22}\end{pmatrix}
$$
with to get the vector
$$
\begin{pmatrix}A_{11} - 4 A_{21} \\ -A_{11} + 4A_{21} \\ A_{12} - 4A_{22} \\ - A_{12} + 4A_{22}\end{pmatrix}
$$
?

 

[jolly_math]

What matrix do you need to multiply the vector
$$
\begin{pmatrix} A_{11} \\ A_{21} \\ A_{12} \\ A_{22}\end{pmatrix}
$$
with to get the vector
$$
\begin{pmatrix}A_{11} - 4 A_{21} \\ -A_{11} + 4A_{21} \\ A_{12} - 4A_{22} \\ - A_{12} + 4A_{22}\end{pmatrix}
$$
?

I think it's a 1x4 matrix, but I can't think of a specific one.

 

[Orodruin]

I think it's a 1x4 matrix, but I can't think of a specific one.

No. You want to map a column vector with 4 entries to another column vector with 4 entries, which type of matrix do you need to use?

 

[jolly_math]

No. You want to map a column vector with 4 entries to another column vector with 4 entries, which type of matrix do you need to use?

A 4x4 matrix?

 

[Orodruin]

A 4x4 matrix?

Why? Can you motivate this answer?

 

[jolly_math]

Why? Can you motivate this answer?

I'm actually not sure why. Could you please explain how

was created? I can't seem to understand it even with hints. Thanks.

 

[Orodruin]

I'm actually not sure why. Could you please explain how View attachment 315074 was created? I can't seem to understand it even with hints. Thanks.

So let us go back to the basics. For a 2x2 matrix
$$
A = \begin{pmatrix} a & b \\ c & d\end{pmatrix}
$$
and a column vector
$$
X = \begin{pmatrix} x \\ y \end{pmatrix},
$$
what is $AX$?

 

[jolly_math]

So let us go back to the basics. For a 2x2 matrix
$$
A = \begin{pmatrix} a & b \\ c & d\end{pmatrix}
$$
and a column vector
$$
X = \begin{pmatrix} x \\ y \end{pmatrix},
$$
what is $AX$?

AX = \begin{pmatrix} ax+by \\ cx+dy\end{pmatrix}

 

[Orodruin]

Right, so what is
$$
\begin{pmatrix}T_{11} & T_{12} & T_{13} & T_{14} \\T_{21} & T_{22} & T_{23} & T_{24} \\T_{31} & T_{32} & T_{33} & T_{34} \\T_{41} & T_{42} & T_{43} & T_{44} \end{pmatrix}
\begin{pmatrix} A_{11} \\ A_{21} \\ A_{12} \\ A_{22}\end{pmatrix}
$$
?

 

[PeroK]

I'm actually not sure why. Could you please explain how View attachment 315074 was created? I can't seem to understand it even with hints. Thanks.

There are (at least) two ways to look at $2 \times 2$ matrices. You can leave the entries in matrix form. Or, you can represent each matrix as a 4D vector. The text makes the following correspondence:
$$
A = \begin{bmatrix} a & b \\ c & d\end{bmatrix} \leftrightarrow (a, b, c, d)
$$This also gives us a correspondence between two reprsentations of the basis matrices/vectors:
$$
A_{11} = \begin{bmatrix} 1 & 0 \\ 0 & 0\end{bmatrix} \leftrightarrow (1, 0, 0, 0) = e_1
$$etc.
Now, take a linear transformation $T$ represented by the matrix
$$
M = \begin{bmatrix} 1 & -1 \\ -4 & 4\end{bmatrix}
$$We can find the action of $T$ on a matrix by matrix multiplication:
$$T(A) = MA$$And, we can find the action on each basis matrix:
$$T(A_{11}) = MA_{11} = A_{11} - 4A_{12}$$etc.
We can also write down the action of $T$ as a linear transformation of our basis vectors $e_1$ etc.
$$Te_1 = e_1 - 4e_2$$etc.
Finally, we can express $T$ as a linear transformation on the vector representation by a $4 \times 4$ matrix. And that is the matrix that so mysteriously appeared in the text.

 

[PeroK]

Right, so what is
$$
\begin{pmatrix}T_{11} & T_{12} & T_{13} & T_{14} \\T_{21} & T_{22} & T_{23} & T_{24} \\T_{31} & T_{32} & T_{33} & T_{34} \\T_{41} & T_{42} & T_{43} & T_{44} \end{pmatrix}
\begin{pmatrix} A_{11} \\ A_{21} \\ A_{12} \\ A_{22}\end{pmatrix}
$$
?

I was working on my reply when you posted this. I did feel the OP was struggling fundamentally with the concept of representing a $2 \times 2$ matrix by a 4D vector.

 

[jolly_math]

Thank you so much, it makes sense now!