Matrix representation of a linear mapping

[JD_PM]

Homework Statement

Is the following statement true or false? If it is the former case, prove it. If it is later, give a counterexample.

Let $n \in \aleph_0$ and $L:\Re^{n} \rightarrow \Re^{n}$ be an injective linear mapping. Let $A \in \Re^{n \times n}$ be an invertible matrix. Then there is a basis $\alpha$ of $\Re^{n}$ and a basis $\beta$ of $\Re^{n}$ such that $A = L_{\alpha}^{\beta}$

Relevant Equations

Please check out diagram

I know that to go from a vector with coordinates relative to a basis $\alpha$ to a vector with coordinates relative to a basis $\beta$ we can use the matrix representation of the identity transformation: $\Big( Id \Big)_{\alpha}^{\beta}$.

This can be represented by a diagram:

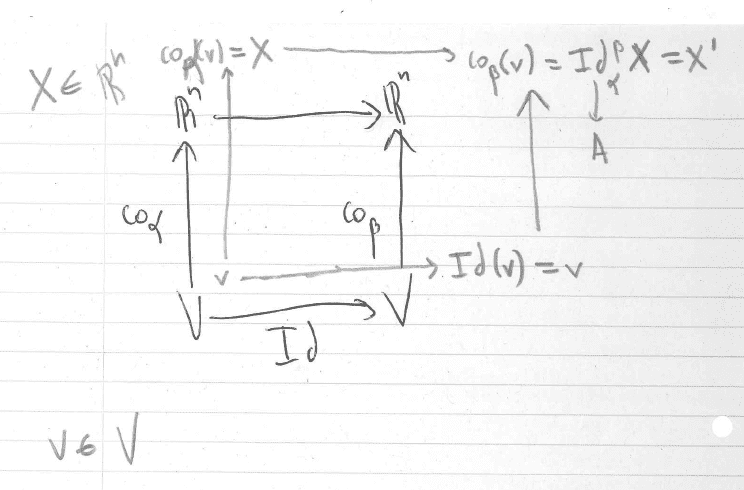
Thus note that the linear mapping we are interested in is $A:X \rightarrow X'$, where:

$$A = \Big( Id \Big)_{\alpha}^{\beta}$$

I think that the statement is true but I think I should use the fact that $A$ is invertible somehow on the above equation in order to prove it. But how?

 

[member 587159]

I think it is true (not entirely sure) , but I think it will take some technical work to prove it. Try to play around with the formula's for change of base and try to come up with "inverse" formulas for them.

 

[vela]

Thus note that the linear mapping we are interested in is $A:X \rightarrow X'$, where:

$$A = \Big( Id \Big)_{\alpha}^{\beta}$$

I think that the statement is true but I think I should use the fact that $A$ is invertible somehow on the above equation in order to prove it. But how?

Interested in for what? How does $L$ fit in here?

 

[JD_PM]

I think it is true (not entirely sure) , but I think it will take some technical work to prove it. Try to play around with the formula's for change of base and try to come up with "inverse" formulas for them.

Alright thanks, I'll think about it and post what I get.

 

[JD_PM]

Interested in for what?

I thought $A:X \rightarrow X'$ was the linear mapping we were interested in because it is the one that involves elements of $\Re^{n}$.

But recently I've been thinking that I shouldn't focus on the elements but in the vector space $\Re^{n}$ itself. In other words: I think I should focus on $L:\Re^{n} \rightarrow \Re^{n}$ instead of $A:X \rightarrow X'$.

 

[HallsofIvy]

Given a linear function, F(X), from R^n->R^m, and bases for both R^n and R^m, then there is a unique matrix with m rows and n columns that represents that function. To find the entries in the matrix, apply the function, F, to each basis vector of R^n in turn, writing the result as a linear combination of the basis vectors of R^m. The coefficients of each such linear combination give one column of the mtatrix.

 

[member 587159]

Given a linear function, F(X), from R^n->R^m, and bases for both R^n and R^m, then there is a unique matrix with m rows and n columns that represents that function. To find the entries in the matrix, apply the function, F, to each basis vector of R^n in turn, writing the result as a linear combination of the basis vectors of R^m. The coefficients of each such linear combination give one column of the mtatrix.

The question does not ask this, but rather the converse. Can you find bases such that a linear transformation has a given matrix?