Problem with series convergence — Taylor expansion of exponential

[Amaelle]

Homework Statement

problem with serie convergence (look at the image)

Relevant Equations

taylor serie expnasion, absolute convergence, racine test

Good day

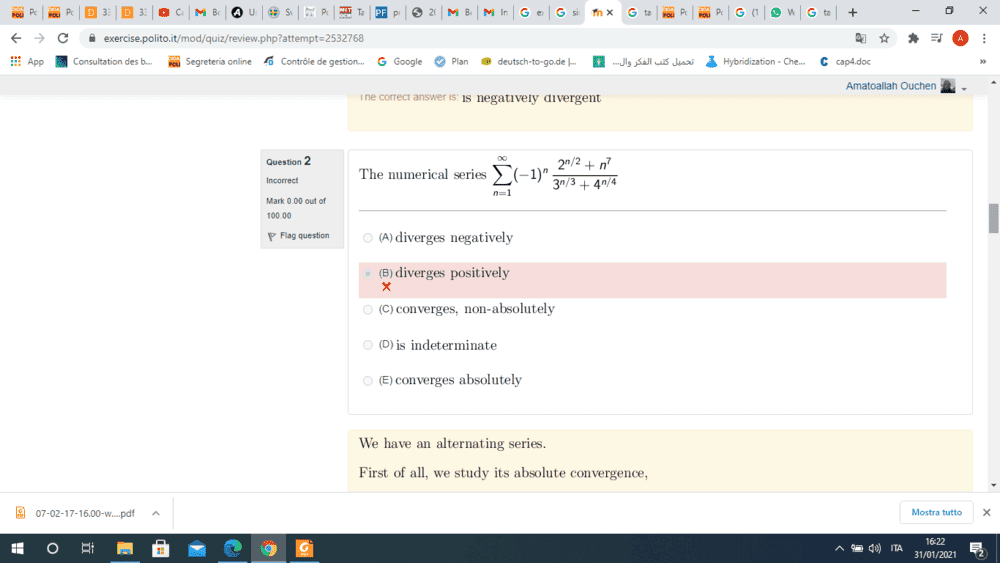
and here is the solution, I have questions about

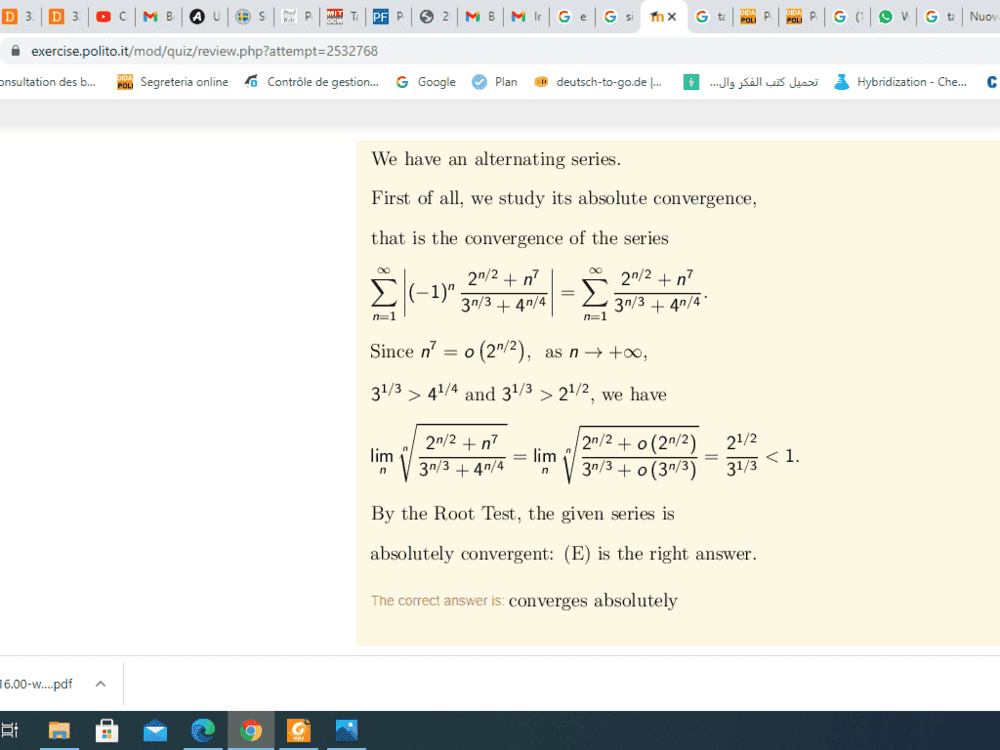
I don't understand why when in the taylor expansion of exponential when x goes to infinity x^7 is little o of x ? I could undesrtand if -1<x<1 but not if x tends to infinity?
many thanks in advance!

 

[suremarc]

$n^7\neq o(n)$. I assume you meant the part where it says $n^7=o(2^{n/2})$. Since $\sqrt{2}>1$, $2^{n/2}$ dominates any power function as $n\rightarrow\infty$.

 

[Amaelle]

Exactely, I would be extremely grateful if you could elaborate more about this point!

 

[suremarc]

Sure. I assume you don’t understand why exponentials dominate power functions? Here is a simple proof: $$\log\frac{n^k}{b^n}=k\log(n)-n\log(b)$$ which tends to $-\infty$ as $n\rightarrow\infty$, provided that $\log(b)>0$. Thus, taking the exponential of both sides shows that $$\lim_{n\rightarrow\infty}\frac{n^k}{b^n}=\lim_{n\rightarrow\infty}e^{k\log(n)-n\log(b)}=0.$$

 

[Amaelle]

thanks a million! you nail it!