Prove that this series converges uniformly on R

[zenterix]

Homework Statement

Prove that the series

$$\sum\limits_{n=1}^\infty \frac{x}{n(1+nx^2)}\tag{1}$$

Relevant Equations

converges uniformly on $\mathbb{R}$.

(Note that the above problem seems relatively straightforward and I think I solved it below. In post 3 is another problem also from Spivak's Calculus, and I haven't been able to solve that one).

Here is the solution I came up with

Consider the sequence of functions $\{f_n\}=\left \{ \frac{x}{n(1+nx^2)}\right \}$ defined on $\mathbb{R}$.

By differentiating $f_n(x)$ and equating to zero we find critical points at $x=\pm \frac{1}{\sqrt{n}}$.

By checking the second derivative we can see that these are the maximum and minimum of $f_n$.

The absolute value of $f_n$ at these two points is the same: $\frac{1}{2n^{3/2}}$.

Therefore, we can say that for all $x\in\mathbb{R}$ we have

$$|f_n(x)|\leq \frac{1}{2n^{3/2}}$$

Consider the sequence $\{ M_n \}=\{\frac{1}{2n^{3/2}}\}$.

Then we can write that for all $x\in\mathbb{R}$ we have

$$|f_n(x)|\leq M_n$$

We can show that $\{M_n\}$ is summable by the integral test.

Therefore, by the Weierstrass M-test, the sequence $\{f_n\}$ is uniformly summable to the function $f(x)=\lim\limits_{n\to\infty} (f_1+\ldots+f_n)$ which is also denoted as $\sum\limits_{n=1}^\infty f_n(x)$.

Here is my attempt at a more intuitive understanding of what is happening.

Here is a plot of $f_1, f_2$, and $f_3$ in red, blue, and green, respectively.

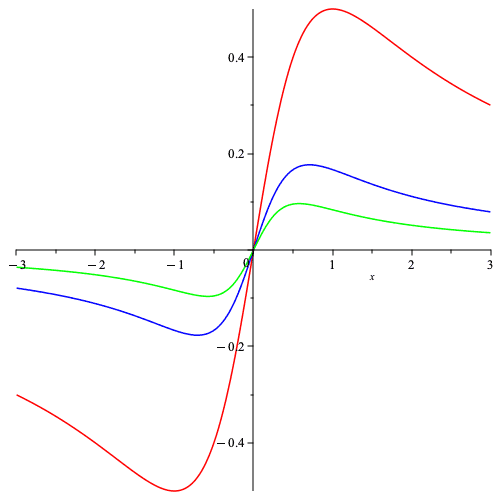
We can see that the sequence of maxima are decreasing and approach zero. In addition, the integral test shows that this sequence is summable.

Now, what we are interested in is the limit $\lim\limits_{n\to\infty} (f_1+\ldots f_n)$ which is a function that we denote as $f(x)=\sum\limits_{n=1}^\infty f_n(x)$.

That is, we are summing graphs such as the three above plus infinite others.

By using the M-test, we ascertained that this sum converges uniformly to $f$.

As far as I can tell, we don't know what this $f$ is exactly though, right?

 

[zenterix]

Here are a few more observations.

- The sequence of maxima is very important. For any $x\in\mathbb{R}$, the sequence $\{|f_n(x)|\}$ is summable by the comparison test with the sequence $\{M_n\}$ (which is itself summable).

- We have this unknown $f(x)=\sum\limits_{n=1}^\infty f_n(x)$. When we consider the difference

$$\left |f(x)-\sum\limits_{n=1}^N f_n(x)\right |$$

we have

$$= \left | \sum\limits_{n=N+1}^\infty f_n(x) \right |$$

$$\leq \sum\limits_{n=N+1}^\infty |f_n(x)|$$

$$\leq \sum\limits_{n=N+1}^\infty M_n$$

The difference between $f$ and the sum of the first $N$ functions $f_n$ is an infinite sum that is smaller than another infinite sum (of $M_n$).

If this other infinite sum exists then the difference can be made as small as desired by making $N$ higher and higher (which removes terms from the sum of $M_n$'s, thus making the infinite sum of these smaller and smaller).

 

[zenterix]

This brings me to another problem that I haven't been able to solve:

Suppose that $f_n$ are nonnegative bounded functions on $A$ and let $M_n=\text{sup}(f_n)$

If $\sum\limits_{n=1}^\infty f_n$ converges uniformly on $A$, does it follow that $\sum\limits_{n=1}^\infty M_n$ converges (a converse to the Weierstrass M-test)?

Once again we have the following.

For all $x\in A$,

$$\left |f(x)-\sum\limits_{n=1}^N f_n(x)\right | = \left | \sum\limits_{n=N+1}^\infty f_n(x) \right |$$

$$\leq \sum\limits_{n=N+1}^\infty |f_n(x)|$$

At this point I just had a little interim in my reasoning to debate with myself about the concepts. I get confused frequently. Here they are.

Given a sequence $\{ a_n\}$, summability is a property related to the convergence of the sequence of partial sums.

Given a sequence $\{ f_n \}$ of functions, summability is the same as the property above when we consider a specific $x$ at which we evaluate the functions in the sequence.

Uniform convergence is related to how the sequence $\{ f_n\}$ behaves at all points in its domain as $n\to\infty$ relative to a specific function $f(x)=\lim\limits_{n\to\infty} f_n(x)$.

Finally, uniform summability has to do with the concept of uniform convergence (as in the above paragraph) but applied to the sequence of partial sums of $\{ f_n \}$.

If that sequence of partial sums converges uniformly to a function $g(x)=\lim\limits_{n\to\infty} \sum\limits_{k=1}^n f_k$ then the original sequence $\{ f_n \}$ is said to be uniformly summable.

Okay, so going back to the problem.
If $\{ f_n \}$ is uniformly summable on $A$, then for any $\epsilon>0$ there is an $N$ such that for any $n>N$ we have that for all $x\in A$

$$\left |f(x)-\sum\limits_{i=1}^n f_i(x)\right |=\left | \sum\limits_{i=n+1}^\infty f_i(x) \right |<\epsilon$$

Okay, so I just spent quite a bit of time thinking and I got nothing for now.

 

[nuuskur]

Suppose that $f_n$ are nonnegative bounded functions on $A$ and let $M_n=\text{sup}(f_n)$

If $\sum\limits_{n=1}^\infty f_n$ converges uniformly on $A$, does it follow that $\sum\limits_{n=1}^\infty M_n$ converges (a converse to the Weierstrass M-test)?

No. The series $\sum \frac{1}{k}I_{[k-1,k]}$ converges uniformly but $\sum \frac{1}{k}$ diverges, as is well known. Here $I_X$ is the indicator/characteristic function on the set $X$.

Otherwise, you've solved the problem. The task is to show the initial series is uniformly convergent, not to try and figure the limiting function. It's not necessarily the case that the limiting function can even be somehow expressed as a finite combination of elementary functions.

 

[WWGD]

Here are a few more observations.

- The sequence of maxima is very important. For any $x\in\mathbb{R}$, the sequence $\{|f_n(x)|\}$ is summable by the comparison test with the sequence $\{M_n\}$ (which is itself summable).

- We have this unknown $f(x)=\sum\limits_{n=1}^\infty f_n(x)$. When we consider the difference

$$\left |f(x)-\sum\limits_{n=1}^N f_n(x)\right |$$

we have

$$= \left | \sum\limits_{n=N+1}^\infty f_n(x) \right |$$

$$\leq \sum\limits_{n=N+1}^\infty |f_n(x)|$$

$$\leq \sum\limits_{n=N+1}^\infty M_n$$

The difference between $f$ and the sum of the first $N$ functions $f_n$ is an infinite sum that is smaller than another infinite sum (of $M_n$).

If this other infinite sum exists then the difference can be made as small as desired by making $N$ higher and higher (which removes terms from the sum of $M_n$'s, thus making the infinite sum of these smaller and smaller).

Nice. Another way of seeing what you wrote in the last line is that the tail of a convergent series goes to 0.