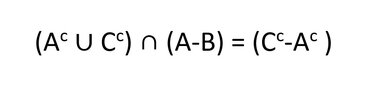Proving Set Operations [Set Theory]

In summary: Next, we need to use the definition of union.That is, we need to define what it means for two sets to be unionized.We can do that by noting that if $A$ and $B$ are unionized, then $A \cup B$ is also unionized.We can also say that if $A$ and $B$ are not unionized, then $A \cap B$ is not unionized.So, in short, $A \cup B$ is the set that contains everything that is in either $A$ or $B$.Finally, we can say that $A \cap B$ is the set that contains everything that is in
  • #1
TheGreat
4
0
Could someone help me in this by simplifying/Proving the equation using Theorems/ Rules on Operation of Sets (i.e Commutative property, idempotent, assoc, dist. , definition of union , def. intersection , DeMorgan ,etc.).

Letting A, B and C be three sets ..

Prove/Disprove :
View attachment 5616
Any solution would be much of help. Hoping to get answers .. Do help me :) Thank you!

I've seen similar questions in here like this:
Problem posted: Prove/Disprove : A−(B∩C) = (A−B)∩(A−C)
soroban said:
Hello, KOO!

We should work on one side of the equation.


[tex]\begin{array}{cccccc}
1. & A -(B \cap C) && 1. &\text{Given} \\
2. & A \cap(B\cup C)^c && 2. &\text{def. Subtr'n} \\
3. & A \cap B^c \cap C^c && 3. & \text{DeMorgan} \\
4. & A \cap A \cap B^c \cap C^c && 4. & \text{Duplication} \\
5. & A\cap B^c \cap A \cap C^c && 5. & \text{Commutative} \\
6. & (A \cap B^c) \cap (A \cap C^c) && 6. & \text{Associative} \\
7. & (A-B) \cap (A-C) && 7. & \text{def. Subtr'n}\end{array}[/tex]

Thank you once again ... Hoping I could get some answer also ..

- jer
 

Attachments

  • problem.jpg
    problem.jpg
    8.5 KB · Views: 96
Last edited:
Physics news on Phys.org
  • #2
TheGreat said:
Could someone help me in this by simplifying/Proving the equation using Theorems/ Rules on Operation of Sets (i.e Commutative property, idempotent, assoc, dist. , definition of union , def. intersection , DeMorgan ,etc.).

Letting A, B and C be three sets ..

Prove/Disprove :
https://www.physicsforums.com/attachments/5616
Any solution would be much of help. Hoping to get answers .. Do help me :) Thank you!

Greetings TheGreat! Welcome to MHB! (Wave)

Let's start by replacing the subtractions by regular set operations.
That is, replace $A-B$ by $A \cap B^c$, and replace $C^c - A^c$ by $C^c \cap (A^c)^c = C^c \cap A$.
It makes it a bit easier to see where the left hand expression should go.
We'll get:
$$ (A^c \cup C^c) \cap (A\cap B^c) \overset?= C^c \cap A$$

Next, let's apply distributivity to the left hand side.
That is, apply the rule that $(P\cup Q)\cap R$ is the same as $(P \cap R) \cup (Q \cap R)$.
Can you? (Wondering)
 
  • #3
I am still a student and I have not yet memorized all theorems on set operations .. I will try to read more on theorems .. Anyway, thank you very much ..
If ever you could prove/disprove it with the full steps, it be very much of a big help :) thanks
 
  • #4
TheGreat said:
I am still a student and I have not yet memorized all theorems on set operations .. I will try to read more on theorems .. Anyway, thank you very much ..
If ever you could prove/disprove it with the full steps, it be very much of a big help :) thanks

Sorry, but we don't usually give full solutions... we believe that is counter productive.
That's why I tried to give as many hints as possible, but we believe a little effort from the poster is required to achieve anything.
If you're not up to showing any effort, or giving any indication where you're stuck, I don't see how we can "really" help you. (Shake)
 
  • #5
ah okay sorry, I am trying to solve it now . Anyway on the LHS, I can't seem to use distributive because operations used inside the parenthesis are union and intersection. How's that?

I like Serena said:
$$ (A^c \cup C^c) \cap (A\cap B^c) \overset?= C^c \cap A$$

Next, let's apply distributivity to the left hand side.
That is, apply the rule that $(P\cup Q)\cap R$ is the same as $(P \cap R) \cup (Q \cap R)$.
 
  • #6
TheGreat said:
ah okay sorry, I am trying to solve it now . Anyway on the LHS, I can't seem to use distributive because operations used inside the parenthesis are union and intersection. How's that?

I like Serena said:
Greetings TheGreat! Welcome to MHB! (Wave)

Let's start by replacing the subtractions by regular set operations.
That is, replace $A-B$ by $A \cap B^c$, and replace $C^c - A^c$ by $C^c \cap (A^c)^c = C^c \cap A$.
It makes it a bit easier to see where the left hand expression should go.
We'll get:
$$ (A^c \cup C^c) \cap (A\cap B^c) \overset?= C^c \cap A$$

Next, let's apply distributivity to the left hand side.
That is, apply the rule that $(P\cup Q)\cap R$ is the same as $(P \cap R) \cup (Q \cap R)$.
Can you? (Wondering)

It means that we pick $P=A^c$, $Q=C^c$, and $R=(A\cap B^c)$.
If we do that, what would $(P \cap R) \cup (Q \cap R)$ look like? (Wondering)
 
  • #7
ah okay , tried distributive and I came up with:
[$A^c$ ∩ (A ∩ $B^c$ )] ∪ [$C^c$ ∩ ( A ∩ $B^c$ )]

what should I do next. Should I use Associative Property to eliminate $A^c$ ∩ A and come up with θ ?
 
  • #8
TheGreat said:
ah okay , tried distributive and I came up with:
[$A^c$ ∩ (A ∩ $B^c$ )] ∪ [$C^c$ ∩ ( A ∩ $B^c$ )]

what should I do next. Should I use Associative Property to eliminate $A^c$ ∩ A and come up with θ ?

Yep! Keep going! (Nod)
 
  • #9
TheGreat said:
Could someone help me in this by simplifying/Proving the equation using Theorems/ Rules on Operation of Sets (i.e Commutative property, idempotent, assoc, dist. , definition of union , def. intersection , DeMorgan ,etc.).

Letting A, B and C be three sets ..

Prove/Disprove :

Any solution would be much of help. Hoping to get answers .. Do help me :) Thank you!

I've seen similar questions in here like this:
Problem posted: Prove/Disprove : A−(B∩C) = (A−B)∩(A−C)Thank you once again ... Hoping I could get some answer also ..

- jer

1st of all if the problem is prove/disprove andvnot only prove ,you should 1st try to disprove the problem, by a counter example because that will save you a lot of unnecessary work.

2ndly the problem that you recalled should read :A−(BUC) = (A−B)∩(A−C) and not

A−(B∩C) = (A−B)∩(A−C)
 
Last edited:
  • #10
I like Serena said:
Yep! Keep going! (Nod)

And how are you going to prove that:

\(\displaystyle A\cap B^c\cap C^c\) it is equal to \(\displaystyle A\cap C^c\) ?
 
  • #11
I like Serena said:
Greetings TheGreat! Welcome to MHB! (Wave)

Let's start by replacing the subtractions by regular set operations.
That is, replace $A-B$ by $A \cap B^c$, and replace $C^c - A^c$ by $C^c \cap (A^c)^c = C^c \cap A$.
It makes it a bit easier to see where the left hand expression should go.
We'll get:
$$ (A^c \cup C^c) \cap (A\cap B^c) \overset?= C^c \cap A$$

Next, let's apply distributivity to the left hand side.
That is, apply the rule that $(P\cup Q)\cap R$ is the same as $(P \cap R) \cup (Q \cap R)$.
Can you? (Wondering)
COUNTER EXAMPLE

If in the above identity of sets we put A=B ,where A and B are non empty and let \(\displaystyle C^c\) be non empty,​then the above equality is not satisfied
 
  • #12
solakis said:
And how are you going to prove that:

\(\displaystyle A\cap B^c\cap C^c\) it is equal to \(\displaystyle A\cap C^c\) ?

Heh. When we have that, we have exactly what we need to set up a counter example to disprove it.
 

FAQ: Proving Set Operations [Set Theory]

What is set theory?

Set theory is a branch of mathematics that deals with the study of sets, which are collections of objects or elements. It is used to define and analyze mathematical concepts such as functions, relations, and numbers.

What are the basic operations in set theory?

The basic operations in set theory are union, intersection, and complement. Union combines two or more sets into one set, intersection finds the common elements between two sets, and complement finds the elements that are in one set but not in another.

How do you prove set operations?

Set operations can be proven using various methods, such as Venn diagrams, algebraic proofs, and logical reasoning. The method used will depend on the specific operation being proven and the level of complexity of the sets involved.

What is the difference between a subset and a proper subset?

A subset is a set that contains all the elements of another set. A proper subset is a subset that is strictly smaller than the original set, meaning it does not contain all the elements of the original set.

Can you give an example of proving set operations?

Yes, for example, to prove that the intersection of two sets A and B is commutative (A ∩ B = B ∩ A), you can use a Venn diagram to show that the common elements between A and B are the same regardless of the order in which you intersect the sets.

Similar threads

MHB Operations on Sets: Proving A⊆B⊆C & A∪B=B∩C
Replies
2
Views
2K
MHB Topology Munkres Chapter 1 exercise 2 b and c- Set theory equivalent statements
Replies
1
Views
1K
I Enumerating a Large Ordinal: Can We Find a Limit to the Continuum?
Replies
27
Views
3K
MHB Proof of Sets: Proving (i) and (ii)
Replies
1
Views
2K
MHB Prove Identities of Sets Hello! (Wave)
Replies
1
Views
1K
MHB How to remember set theory properties?
Replies
4
Views
2K
MHB Proving Symmetric Difference Properties of Sets
Replies
1
Views
2K
Set Theory: Power sets of Unions
Replies
3
Views
1K
Proving Basic Set Theory: Trichotomy, Union, Intersection, and Multiplication
Replies
5
Views
5K
Let A, B and C be sets. Prove that
Replies
2
Views
3K

Hot Threads

Recent Insights

Back
Top