- #1
mathmari
Gold Member
MHB
- 5,049
- 7
Hey! 
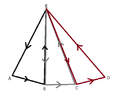
View attachment 2092
$\overrightarrow{F}=M \hat{i}+ N \hat{j}+ P \hat{k}$
To prove the Stokes' Theorem we apply Green's Theroem at $ABE$, $BCE$, $CDE$.
$(\oint_{ABE}+\oint_{BCE}+\oint_{CDE}){ \overrightarrow{F}}d \overrightarrow{R}=\iint_{ABCDE}{ \nabla \times \overrightarrow{F} \cdot \hat{n}}d \sigma$
$(\oint_{ABE}+\oint_{BCE}+\oint_{CDE}){ \overrightarrow{F} }d \overrightarrow{R}=\oint_{ABCDE}{\overrightarrow{F}}d \overrightarrow{R}+\int_B^E{\overrightarrow{F}}d \overrightarrow{R}+\int_E^B{\overrightarrow{F}}d \overrightarrow{R}+\int_C^E{\overrightarrow{F}}d \overrightarrow{R}+\int_E^C{\overrightarrow{F}}d \overrightarrow{R}=\oint_{ABCDE}{\overrightarrow{F}}d \overrightarrow{R}$
Isn't the Green's Theorem:
$\oint_S{\overrightarrow{F} d \overrightarrow{R}}=\iint_R{\nabla \times \overrightarrow{F} dA}$?
Is this the same as $\iint_{ABCDE}{ \nabla \times \overrightarrow{F} \cdot \hat{n}}d \sigma$?
View attachment 2092
$\overrightarrow{F}=M \hat{i}+ N \hat{j}+ P \hat{k}$
To prove the Stokes' Theorem we apply Green's Theroem at $ABE$, $BCE$, $CDE$.
$(\oint_{ABE}+\oint_{BCE}+\oint_{CDE}){ \overrightarrow{F}}d \overrightarrow{R}=\iint_{ABCDE}{ \nabla \times \overrightarrow{F} \cdot \hat{n}}d \sigma$
$(\oint_{ABE}+\oint_{BCE}+\oint_{CDE}){ \overrightarrow{F} }d \overrightarrow{R}=\oint_{ABCDE}{\overrightarrow{F}}d \overrightarrow{R}+\int_B^E{\overrightarrow{F}}d \overrightarrow{R}+\int_E^B{\overrightarrow{F}}d \overrightarrow{R}+\int_C^E{\overrightarrow{F}}d \overrightarrow{R}+\int_E^C{\overrightarrow{F}}d \overrightarrow{R}=\oint_{ABCDE}{\overrightarrow{F}}d \overrightarrow{R}$
Isn't the Green's Theorem:
$\oint_S{\overrightarrow{F} d \overrightarrow{R}}=\iint_R{\nabla \times \overrightarrow{F} dA}$?
Is this the same as $\iint_{ABCDE}{ \nabla \times \overrightarrow{F} \cdot \hat{n}}d \sigma$?