Question about band gaps in 2D

[emily1986]

I'm studying a two dimensional lattice with delta functions at the lattice points. When I diagonalized the hamiltonian I noticed that if I kept the dimension of my matrix less than 5 I would get band gaps at all the BZ boundaries. However, if I increased my matrix to a dimension 5 or higher, some of the bands never got a band gap at certain boundaries despite a huge potential! The picture shows the first 5 energy bands (used dimension 9 matrix because it is more symmetric along the diagonal) for a .5 potential in atomic units.

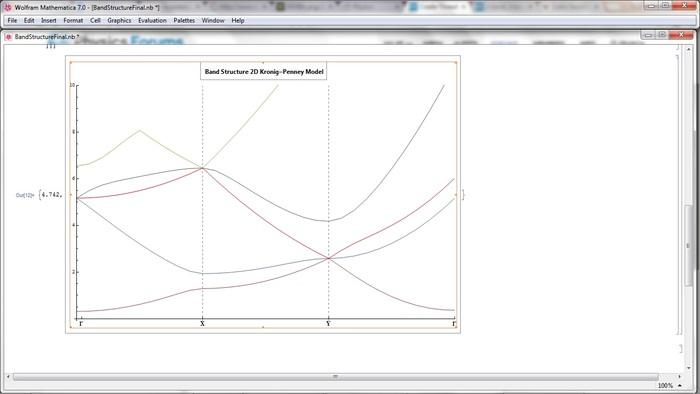
So I was trying to figure out why this was happening, and I thought that perhaps it's because the roots of 5th order polynomials and higher can't be expressed in terms of radicals. This is a stretch, but maybe the potential-dependent separation between bands at the BZ boundaries is in part a result of having radicals in the solution to the eigenvalues problem. This doesn't happen when using a 1D lattice however, so why would radicals only matter in 2D?

My other guess is that it has something to do with symmetry breaking. Perhaps the symmetry isn't broken at these points for some reason. I wouldn't know how to back this up however. Could anyone tell me why there are no band gaps at some locations for a hamiltonian 5x5 and higher?

Thank you!

 

[DrDu]

How do you implement the 2d Delta functions? I think this is highly nontrivial, as delta potentials for d>1 require renormalisation.

 

[emily1986]

DrDu,

I diagonalize the hamiltonian in reciprocal space so the off-diagonal terms are just constants.

 

[DrDu]

Not quite sure what you mean.

 

[emily1986]

Band structure is plotted as energy vs. reciprocal lattice vectors k. To find the eigenvalues as a function of k, the hamiltonian needs to be expressed in reciprocal space. This means that we take need to take the Fourier transform of the delta functions which results in some chosen constant V in all of the off-diagonal spaces of our matrix.

 

[DrDu]

Yes, ok, but this will only be exact in the limit V to infinity.
Anyhow this kind of delta function should have no influence on the spectrum, so I am not surprised of your result.
Why don't you try a potential $V=\sum_i \delta(x-ia)+\sum_j \delta(y-ja)$?

 

[emily1986]

The delta function in 2D is V=(∑iδ(x−ia))(∑jδ(y−ja)) The sums must be multiplied together in order to form a square lattice.

Also, the potential does has an influence on the spectrum, but only at certain points. You can see from the picture I posted that there are bands gaps, just not at every symmetry point.

One more thing, V is infinity in real space, but in reciprocal space it is only a constant. So the solution is exact.

 

[DrDu]

I know, but the sum will lead to a well defined solvable lattice structure, however with delta functions on the corners of the unit cell.
If your potential has an influence on the spectrum, I would suspect this to be artifacts of the approximation you are making.
Could you transform your potential back to real space for, say, a 5x5 lattice?

 

[emily1986]

By approximation do you mean limiting the size of my matrix?

 

[DrDu]

By approximation do you mean limiting the size of my matrix?

Yes, if you use a lattice with only N atoms in each direction, you will get some sinc functions, instead of deltas.

 

[emily1986]

How would changing my potential back to real space fix this? Wouldn't it just make things more complicated? My matrix would still have N dimensions so I wouldn't be removing any approximations.

 

[DrDu]

It wouldn't, I just thought you may want to check what potential you are dealing with in reality.

 

[emily1986]

I don't understand what you are getting at. My potential in real space is just a product of two delta functions summed over all lattice vectors. The Fourier transform of a delta function will be a constant regardless of the dimension of my matrix.

 

[DrDu]

Ok, let's start anew, as I did not remember some things correctly about delta functions in 2 and 3d.
Are the delta potentials positive or negative?
Could you provide a complete expression for the truncated hamiltonians you are diagonalizing?

 

[emily1986]

Sure. Here is an example 9x9 matrix. The potential V can be any value. Units are atomic.

 

[DrDu]

I understand some of the degeneracy at at the high symmetry points. E.g. the states (Kx,Ky)=(1,0) and (0,1) span a two dimensional representation of the little group ($C_{4v}$?) at Gamma. What are the k-vectors corresponding to X and Y, I guess (1/2,0) and (1/2,1/2) but which is which?

 

[emily1986]

That's right. X corresponds to point (.5,0) and Y corresponds to (.5,.5)

 

[DrDu]

What I also don't understand: The spectrum at Gamma on the left of your graphics is not identical to that on the right.

 

[emily1986]

Yeah the graph is skewed for some reason. Here is a better version.

 

[DrDu]

Ok, so I am starting to get an idea how to qualitatively interpret your results: Easiest is the situation V=0. E.g. at point Y,
the following states are degenerate (degenerate levels ordered according to energy): [(-1,0), (0,0),(0,-1),(-1,1)], [(1,0),(0,1),(1,-1),(-1,1)],(1,1) where the brakets are (Kx,Ky). Now using degenerate perturbation theory, each of the 4 blocks is split into a 3+1 states where the single state is shifted upwards, because a nxn matrix filled with ones, has one eigenvalue n and n-1 eigenvalues 0. The same can be done for the other high symmetry points (it would be more standard to relabel Y to M).

For larger values of V, I would expect only some 2 fold degeneracies to remain. The next step would be to label the zeroth order states at the high symmetry points according to the symmetry of the little group.

 

[DrDu]

Nice article on the subject:
http://large.stanford.edu/courses/2007/ap272/laughlin2/

 

[emily1986]

[(-1,0), (0,0),(0,-1),(-1,1)], [(1,0),(0,1),(1,-1),(-1,1)],(1,1)

It seems like you have found the crux of the issue, but I don't quite understand yet. Would you mind explaining your previous post in more detail? For instance, what exactly is being represented by these sets of numbers? The (-1,0) represents the x and y components of a reciprocal lattice vector, but why do you have them in groups of 4? Is the last ordered pair a typo? I also don't see how they are degenerate.

Now using degenerate perturbation theory, each of the 4 blocks is split into a 3+1 states where the single state is shifted upwards, because a nxn matrix filled with ones, has one eigenvalue n and n-1 eigenvalues 0. The same can be done for the other high symmetry points (it would be more standard to relabel Y to M).

It's starting to make sense! I played around with some random matrices to confirm what you said here. If the matrix has all the same elements along the diagonal, i.e. all degenerate, and the same constant for all the off-diagonals, then only one band is affected by the off-diagonals. If the off-diagonals are positive, then this will be the top band. If they are negative, this will be the smallest band. I tried changing my potential to a negative value, and indeed the lowest band separated from the rest instead of the top band. I'm not sure how this relates to degenerate perturbation theory, but maybe it will make more sense once I review my notes on that topic.

 

[DrDu]

I meant that the diagonal elements can be written as $(Kx+kx)^2+(Ky+ky)^2$. At the gamma point, kx=ky=0. I grouped degenerate states with square brakets.
The eigenstate corresponding to the eigenvalue n of an nxn matrix of ones is (1 1 1 ...1). All what is orthogonal corresponds to eigenvalue 0.