Riesz Basis Problem: Definition & Problem Statement

[ashah99]

Homework Statement

Determine if {phi(t-n)} is a Riesz basis for the space V = Span({phi(t-n)})

Relevant Equations

The definition of the Riesz basis used for this problem is included below.

The reference definition and problem statement are shown below with my work shown following right after. I would like to know if I am approaching this correctly, and if not, could guidance be provided? Not very sure. I'm not proficient at formatting equations, so I'm providing snippets, my apologies. Thank you.

Problem:

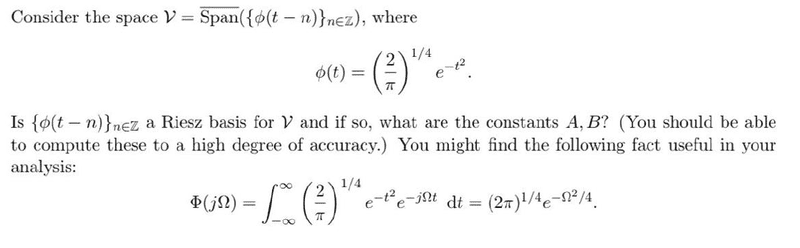
My attempt at a solution:

 

[Office_Shredder]

I'm a little confused right at the start. Where did the $\alpha_n$ go? It looks like you replaced them with some functions of t, but I think they're just supposed to be arbitrary constants.

 

[ashah99]

I'm a little confused right at the start. Where did the $\alpha_n$ go? It looks like you replaced them with some functions of t, but I think they're just supposed to be arbitrary constants.

I was not sure how to begin so I used the functions given. How can I go about solving this correctly?

 

[WWGD]

I haven't read in detail but I suspect one or both of Cauchy-Schwatz, Holder or similar inequalities should be needed.

 

[Keith_McClary]

There is a Wikipedia . I don't understand how translated Gaussians can be a basis - I assumed they couldn't.

 

[Office_Shredder]

There is a Wikipedia . I don't understand how translated Gaussians can be a basis - I assumed they couldn't.

The vector space is defined to be the span of those functions, so kind of definitionally they form a basis unless they are linearly dependent.

So let's recall some definitions. I'm assuming things are over the reals, is it's over the complex numbers just add some complex conjugates as needed. I think it doesn't affect anything.

$$\left< \phi(t-m), \phi(t-n\right> = \int_{-\infty}^{\infty} \sqrt{\frac{2}{\pi}} e^{-(t-m)^2}e^{-(t-n)^2} dt$$
$$||\sum_{k\in \mathbb{Z}} \alpha_k \phi(t-k)||^2 = \left< \sum_{m\in \mathbb{Z}} \alpha_m \phi(t-m), \sum_{n\in \mathbb{Z}} \alpha_n \phi(t-n) \right>$$

By linearity of the inner product, and assuming the necessary sums actually converge,this is equal to
$$\sum_{m,n\in \mathbb{Z}} \alpha_m \alpha_n \left<\phi(t-m),\phi(t-n)\right>$$

If the $\phi(t-k)$s formed an orthonormal basis, then $\left<\phi(t-m),\phi(t-n)\right>$ is 0, except for when $m=n$ in which case you get 1. So that sum would always be exactly equal to
$$\sum_{k\in\mathbb{Z}} \alpha_k^2$$.

Of course they are not orthonormal. But if they form a Riesz basis, they are almost orthonormal, which means the norm squared is always
$$C\sum_{k\in\mathbb{Z}} \alpha_k^2$$

For some $A\leq C\leq B$ (where C will be different for different choices of $\alpha_k$)

 

[ashah99]

The vector space is defined to be the span of those functions, so kind of definitionally they form a basis unless they are linearly dependent.

So let's recall some definitions. I'm assuming things are over the reals, is it's over the complex numbers just add some complex conjugates as needed. I think it doesn't affect anything.

$$\left< \phi(t-m), \phi(t-n\right> = \int_{-\infty}^{\infty} \sqrt{\frac{2}{\pi}} e^{-(t-m)^2}e^{-(t-n)^2} dt$$
$$||\sum_{k\in \mathbb{Z}} \alpha_k \phi(t-k)||^2 = \left< \sum_{m\in \mathbb{Z}} \alpha_m \phi(t-m), \sum_{n\in \mathbb{Z}} \alpha_n \phi(t-n) \right>$$

By linearity of the inner product, and assuming the necessary sums actually converge,this is equal to
$$\sum_{m,n\in \mathbb{Z}} \alpha_m \alpha_n \left<\phi(t-m),\phi(t-n)\right>$$

If the $\phi(t-k)$s formed an orthonormal basis, then $\left<\phi(t-m),\phi(t-n)\right>$ is 0, except for when $m=n$ in which case you get 1. So that sum would always be exactly equal to
$$\sum_{k\in\mathbb{Z}} \alpha_k^2$$.

Of course they are not orthonormal. But if they form a Riesz basis, they are almost orthonormal, which means the norm squared is always
$$C\sum_{k\in\mathbb{Z}} \alpha_k^2$$

For some $A\leq C\leq B$ (where C will be different for different choices of $\alpha_k$)

So, the next step solving the question is just showing the 2nd condition of the Wikipedia page, Σ_{n ∈ ℤ} | F{ϕ}(2πn + ω) |^2 for some A, B > 0? Not sure how to go about this.

 

[ashah99]

Retrying this problem using the suggested Riesz sequence - Wikipedia link above, sorry for quality:

This is how far I got, but now stuck on using Fourier transform properties. Any ideas to proceed?

 

[Office_Shredder]

I think I can do one direction, and it didn't require any equivalence theorem, but it was slightly non obvious. The other direction eludes me but is probably similar.Let's start with the simple step. Can you compute
$$\left<\phi(t-m),\phi(t-n)\right>$$

Edit to add: actually the other direction is basically the same. There's just one epsilon-clever trick I think once you compute the inner products to get over the finish line here. I doubt I got the optimal constants though.

 

[Delta2]

and it didn't require any equivalence theorem

Judging by the hint given (the Fourier transform $\Phi(\Omega)$ of $\phi (t)$) can't we say that the problem want us to make use of the equivalence theorem?

Does your method use the hint?

 

[Office_Shredder]

Judging by the hint given (the Fourier transform $\Phi(t)$ of $\phi (t)$) can't we say that the problem want us to make use of the equivalence theorem?

Does your method use the hint?

Oh that's funny, I thought the hint was just telling you in a roundabout way how to compute the inner product of two of these things. I guess this makes more sense to me why you would use this theorem on Wikipedia now.