- #1
Amaelle
- 310
- 54
- Homework Statement
- Look at the image
- Relevant Equations
- Absolute convergence.
Greetings
here is the exercice
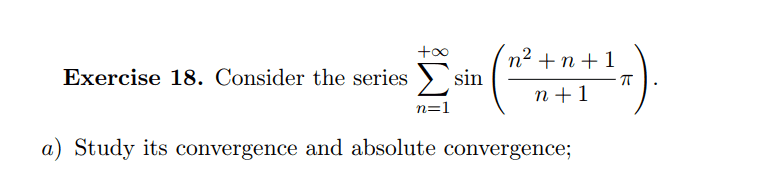
My solution was
as n^2+n+1/(n+1) tends asymptotically to n then the entire stuffs inside the sinus function tends to npi which make it asymptotically equal to sin(npi) which is equal to 0 and consequently the sequence is Absolutely convergent
Here is the solution of the book
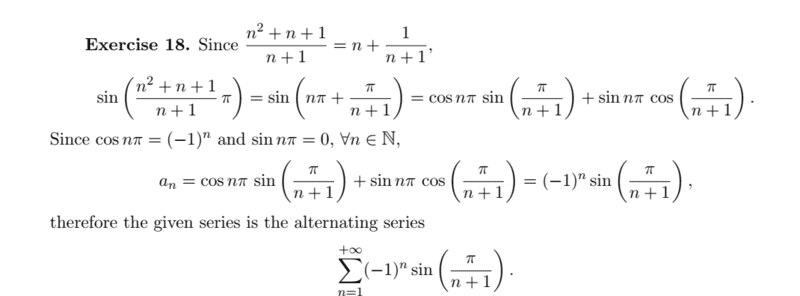
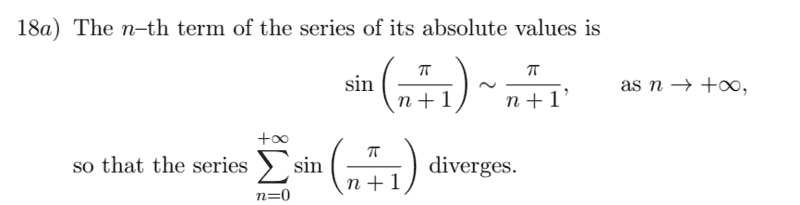
I do unsderstand it very well but I need to know where my logics has failed me in my attempt
thank you!
here is the exercice
My solution was
as n^2+n+1/(n+1) tends asymptotically to n then the entire stuffs inside the sinus function tends to npi which make it asymptotically equal to sin(npi) which is equal to 0 and consequently the sequence is Absolutely convergent
Here is the solution of the book
I do unsderstand it very well but I need to know where my logics has failed me in my attempt
thank you!