- #1
Amaelle
- 310
- 54
- Homework Statement
- Let Σ = [(x, y, z) ∈ R3 : z=-1/4+√(x^2+y^2) 0 <= z<=1/2]
be a surface oriented
so that the normal versor of Σ forms an obtuse angle with the fundamental versor of the z–axis.
Compute the flux of the curl of the vector field
F(x, y, z) = 2yz *exponontiel(x^2+z^2),3z*exponontiel(x^2+y^2),(0,5x+z)exponontiel(x^2+y^2)
- Relevant Equations
- Divergence theorem
Good day all
my question is the following
Is it correct to (after calculation the new field which is the curl of the old one)to use the divergence theroem on the volume shown on that picture?
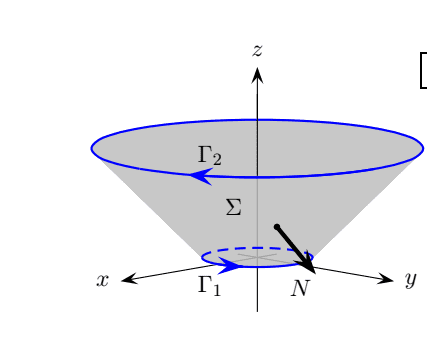
The divergence theorem should be applied on a closed surface , can I consider this as closed?
Thanks a lot!
my question is the following
Is it correct to (after calculation the new field which is the curl of the old one)to use the divergence theroem on the volume shown on that picture?
The divergence theorem should be applied on a closed surface , can I consider this as closed?
Thanks a lot!
Attachments
Last edited by a moderator: