- #1
big dream
a microchannel of length 2L and width h in the thermal cycling region. the temperature profile
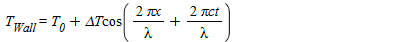 ...(1)
...(1)
the cyclic temperature profile leads to a time dependent density
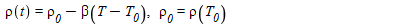 ...(2)
...(2)
using the mass conservation equation i.e.
 ...(3)
...(3)
and momentum balance equation i.e.
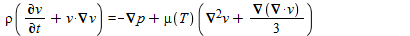 ...(4)
...(4)
we have to find the exact solution of u, v & p
The attempt at a solution
equ(1) →

equ(2) →
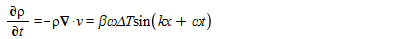
length scales are normalised as
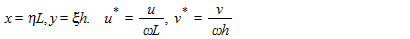
so equ(2) becomes
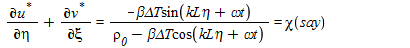
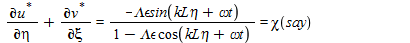
no slip & no penetration boundary condition at the walls (y=0,h) ; and constant pressure at channel entrance(x=-L) and exit(x=L). for small reynolds number eq(3) becomes

this equation normalised as

as

and from

we can get
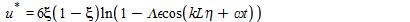
&
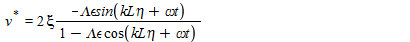 is it the right process?
is it the right process?
the cyclic temperature profile leads to a time dependent density
using the mass conservation equation i.e.
and momentum balance equation i.e.
we have to find the exact solution of u, v & p
The attempt at a solution
equ(1) →
equ(2) →
length scales are normalised as
so equ(2) becomes
no slip & no penetration boundary condition at the walls (y=0,h) ; and constant pressure at channel entrance(x=-L) and exit(x=L). for small reynolds number eq(3) becomes
this equation normalised as
as
and from
we can get
&
Attachments
-
 upload_2017-10-30_14-21-20.png1.2 KB · Views: 1,114
upload_2017-10-30_14-21-20.png1.2 KB · Views: 1,114 -
 upload_2017-10-30_14-22-42.png915 bytes · Views: 1,125
upload_2017-10-30_14-22-42.png915 bytes · Views: 1,125 -
 upload_2017-10-30_14-23-38.png523 bytes · Views: 800
upload_2017-10-30_14-23-38.png523 bytes · Views: 800 -
 upload_2017-10-30_14-25-21.png1.3 KB · Views: 1,076
upload_2017-10-30_14-25-21.png1.3 KB · Views: 1,076 -
 upload_2017-10-30_14-29-10.png978 bytes · Views: 1,048
upload_2017-10-30_14-29-10.png978 bytes · Views: 1,048 -
 upload_2017-10-30_14-29-35.png1.1 KB · Views: 1,060
upload_2017-10-30_14-29-35.png1.1 KB · Views: 1,060 -
 upload_2017-10-30_14-30-20.png916 bytes · Views: 1,054
upload_2017-10-30_14-30-20.png916 bytes · Views: 1,054 -
 upload_2017-10-30_14-30-55.png1.8 KB · Views: 1,079
upload_2017-10-30_14-30-55.png1.8 KB · Views: 1,079 -
 upload_2017-10-30_14-37-9.png443 bytes · Views: 1,039
upload_2017-10-30_14-37-9.png443 bytes · Views: 1,039 -
 upload_2017-10-30_14-45-34.png675 bytes · Views: 1,027
upload_2017-10-30_14-45-34.png675 bytes · Views: 1,027 -
 upload_2017-10-30_14-49-1.png842 bytes · Views: 1,064
upload_2017-10-30_14-49-1.png842 bytes · Views: 1,064 -
 upload_2017-10-30_14-49-22.png646 bytes · Views: 1,059
upload_2017-10-30_14-49-22.png646 bytes · Views: 1,059 -
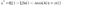 upload_2017-10-30_14-51-27.png1.1 KB · Views: 1,014
upload_2017-10-30_14-51-27.png1.1 KB · Views: 1,014 -
 upload_2017-10-30_14-53-56.png1.1 KB · Views: 1,055
upload_2017-10-30_14-53-56.png1.1 KB · Views: 1,055 -
 upload_2017-10-30_14-55-45.png1.6 KB · Views: 1,067
upload_2017-10-30_14-55-45.png1.6 KB · Views: 1,067





