Volume of Revolution for Polynomial Bowl

[reybob]

Homework Statement

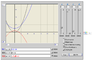
The question asked is to make a bowl out of polynomial equations rotated around the y axis. The bottom of the bowl has to have a maximum at the center and a minimum at some distance from the center.

The equations I want to use are x^2+10, 1.3x^2 and -.7x^2 + 4.

The problem I face is what to do about the bottom of the bowl, since it is comprised of 2 functions meeting to form a minimum. Should I treat those two as its own volume of revolution, find the volume and then subtract the interior (top of bowl) from that total?

Homework Equations

Disc method: pi*integ: r(y)^2 dy

The Attempt at a Solution

pi*Integ: ((y-10)^1/2)^2 - [pi*Integ: ((y/1.3)^1/2)^2 - ((y-4/.7)^1/2)^2]

Is my attempt correct? The volume I am trying to find is bounded by x=0 (the y axis) and the 3 other equations

 

[nickalh]

Does this exercise allow us our own equations?
Why not simplify it with?
"y= x^2/2+30,y=1/8 x^4 -x^2 +5"
This allows us one integral with shell method.If that's not allowed, we'll need at least two separate integrations.
Are you required disc/ washer method? I think this exercise is easier with shell method on your equations. Then it can be done with only two integrals.

Disc/ washer method will require 3 separate integrals.
all numbers are approximate, but must be found exactly or more precisely before integrating.
The limits of integration
y:2.5->4 washer method
y:4->10 disk method
y:10->45 washer method
For washer method it's always pi[(outer radius)^2 - (inner radius)^2]
Disk method is a simplification of the same formula, with inner radius =0.Either way, we definitely need limits of integration.
Without limits of integration, I can't tell how close you are to an effective method.

 

[reybob]

We can use our own, I going to take your advice and use those equations! I couldn't find a curve that looked like that, this is much easier to work with! Thank you so much, this makes my life much easier!

 

[nickalh]

I knew some 4th degree function had the desired behavior. I just played around with wolframAlpha.com until I had the right graph.

An even function is symmetric on both sides of the y axis.
So only x^2 & x^4, & constant terms.

I first tried x^4 +x^2 with various coefficients but that did not give any of the needed humps. Then I realized x^4 term & x^2 needed to go the opposite direction. From there I just fine tuned the coefficients until it looked nice.

WolframAlpha.com is the best thing since sliced bread. Nearly instant graphing, less strict syntax to learn.

Have fun in your learning.