yucheng
- 232
- 57
Hi!
This thread might well be similar to:
https://www.physicsforums.com/threa...classical-electrodynamics-3rd-edition.910410/
I'm self-studying Vanderlinde and having a great time. However, I think that I am conflating and confusing many different things. Let me just ask them here:
Chapter 5 Laplace's equations.
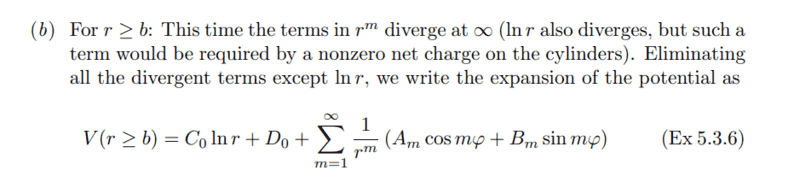
Thanks in advance!
This thread might well be similar to:
https://www.physicsforums.com/threa...classical-electrodynamics-3rd-edition.910410/
I'm self-studying Vanderlinde and having a great time. However, I think that I am conflating and confusing many different things. Let me just ask them here:
Chapter 5 Laplace's equations.
- When solving the equation, ending in a series expansion, in what domain is the expansion valid?
The potential is specified for side 4, while the other sides are set to zero. From what I know of, the potential is a harmonic function i.e. it takes on a maximum or a minimum at the boundaries. Does this mean that the solution I have found is only valid within the boundary? I think so.
But then, you can specify two disconnected, nested boundaries like the circle as the lower bound to the radial distance, and infinity.
So, the author arrives at the equation
So, where is equation 5-15 valid? It can be used for both the region within and the region outside of the parallelepiped right, as long as the boundary conditions are specified (and delineates the bounding region)? - On page 93, Vanderlinde mentions that we are solving for static fields with charges on the boundary. For problems where a potential is specified on a conductor, find the potential in space, fields etc., does this mean that the equation is only valid for the region of interest, but not the conductor?
- In Example 5.3 on page 100, the author gives coaxial nonconducting cylinders with surface charge densities giving rise to potential, and solves the Laplace's equation by specializing V with r = a.
But doesn't this mean that ##\nabla^2 V \neq 0 ## anymore, at least on the boundary? So... why are we not solving Poisson's equation instead, with a dirac delta function for the charge density, of course?
- Why is ##\ln r## needed to to have a nonzero net charge?
Thanks in advance!