kev said:
First, I wish to understand the physical meaning of s or ds in this context. From the Schwarzschild metric it would appear to be ds = c*dtau where tau is the proper time, but the proper time according to whom? If we are measuring the distance from coordinate radius r1 to r2 is it the proper time according to:
a) A stationary observer located at r1?
b) A stationary observer located at r2?
c) An observer free falling from r2 to r1?
d) The sum of infinitesimal proper time intervals made by a large number of stationary observers spread out from r1 to r2?
I was a bit lax in my notation, and this is indeed a bit of a notational grey area.
To keep things simple, let's just consider flat 2-d spacetime (i.e. 1 space + 1 time coord, with no gravity). Different authors will tell you that the metric is given by one of the following equations.
ds^2 = c^2 dt^2 - dx^2 (I)
ds^2 = dt^2 - dx^2 / c^2 (II)
ds^2 = dx^2 - c^2 dt^2 (III)
ds^2 = dx^2 / c^2 - dt^2 (IV)
(I) and (II) are referred to as a (+---) metric signature, while (III) and (IV) are referred to as a (-+++) signature. When you get more experienced in the subject, you might even mentally switch from one definition to another without explicitly saying so.
What is
s? Well you have to measure it along a curve in spacetime, and it depends what sort of curve it is.
If the curve is a timelike curve, i.e. represents the wordline of a particle, then equation (II) gives you the proper time s = \tau experienced by that particle.
(By the way, use "\tau" in tex.) Equivalently equation (I) gives you s = c\tau, and rather more uglier, (III) gives you s = ic\tau and (IV) gives you s = i\tau.
On the other hand, if the curve is spacelike and lies within the surface of simultaneity of an observer, then equation (III) gives you the distance
s = d along that curve, according to that observer (with appropriate variants for the other metric equations I-IV). In GR this has to be modified slightly to say that the distance is measured using local rulers, i.e. at each point along the curve you use a local observer at that point to make the infinitesimal measurement
ds. The curve has to lie parallel to each local observer's surface of simultaneity at that point, in other words, each local observer is stationary relative to the line in space being measured.
(If the curve is null or lightlike,
s = 0, and the curve is the worldline of a photon.)
In my previous post, I was implicitly assuming the (III) version of the metric, because that version is more convenient for measuring distance as opposed to time. By putting
dt = 0 I was using the metric to measure distance along a spacelike curve rather than time.
(It might have been less confusing if I'd used a different letter e.g.
d instead of
s to denote ruler distance. Then, using the metric signature (I) that you had used in previous posts,
d = is.)
Does that make more sense now?
kev said:
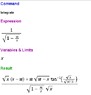
Could you show how equation (5) is obtained?
From my original equation (4)
dZ = 2 \sqrt{r_s} \cdot \frac{1}{2}(r - r_s)^{-1/2} dr
dZ^2 = \frac {r_s}{r - r_s} dr^2
dr^2 + dZ^2 = \frac{(r-r_s) + r_s}{r - r_s} dr^2
dr^2 + dZ^2 = \frac{dr^2}{1 - r_s/r}
(It is also possible to work backwards to obtain (4) from (5), which is what I originally did.)
kev said:
On the other hand a finite "distance" to the event horizon does not necessarily mean it can be reached in a finite time.
Indeed. It depends which "time" you mean. For the Schwarzschild coordinate time
t, or the time of any "stationary" observer, it takes an infinite time. But in the traveller's proper time \tau, it takes a finite time. The difference is due to gravitational time dilation (which isn't included in the "Schwarzschild parabola" space-only visualisation).
 Orbiting satellites do seem to provide a big easy-to-observe natural clock for comparisons. Only trouble is, there are no natural stable orbits below the photon horizon , maybe slightly higher?
Orbiting satellites do seem to provide a big easy-to-observe natural clock for comparisons. Only trouble is, there are no natural stable orbits below the photon horizon , maybe slightly higher?