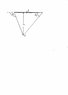
Yes. If you're interested in the field at a point P, which may be anywhere outside the wire, the B-S rule gives you the field at P due to each current element. You integrate these field contributions from the whole wire. This gives you (see thumbnail for meaning of symbols):
B = \frac{\mu_0 I}{4\pi a} [cos \theta_2 - cos \theta_1].
This covers the cases you're interested in; it's very general.
For a very long wire, if P is outside the wire, near the middle of the wire, then \theta_2 = 0, \theta_1 = \pi, so B = \frac{\mu_0 I}{2\pi a}, whereas if you're outside the wire, at the (left hand) end of the wire, \theta_2 = 0, \theta_1 = \frac{\pi}{2}, so B = \frac{\mu_0 I}{4\pi a}. If you think about it, you would indeed expect the field to be half as much in the second case as in the first - if you appreciate that the exact length of the wire is immaterial in these 'long wire' examples, because the field from distant parts of the wire is negligible.
Remember that you can't, in practice, have a wire which carries a steady current and which has two free (unconnected) ends. The wire needs to be part of a circuit. For the second case above, the left hand end of the wire would have to be connected to the rest of a circuit by another wire. If this other wire went in the direction directly away from P it wouldn't contribute to the field at P. Can the rest of the circuit (apart from the straight wire) be made so as not to contribute to the field at P?