chiefjslay
- 4
- 0
Im stuck on this problem and I've gotten to the point where I am just staring at my computer, so I figured Id give you guys a go at it.
I got Part A which was fairly simple. But I've tried everything but can't seem to get Part B. I must be missing something. This is one of those online assignments where you get as many attempts as you want. I keep getting Part A, but can't get Part B. Please explain how you did Part B if you get it. I have the correct answers too.
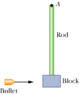
In Fig. 11-52, a 7.3 g bullet is fired into a 0.46 kg block attached to the end of a 0.12 m nonuniform rod of mass 0.88 kg. The block-rod-bullet system then rotates in the plane of the figure, about a fixed axis at A. The rotational inertia of the rod alone about A is 0.038 kg·m2. Treat the block as a particle. (a) What then is the rotational inertia of the block-rod-bullet system about point A? (b) If the angular speed of the system about A just after impact is 7.2 rad/s, what is the bullet's speed just before impact?
I got Part A which was fairly simple. But I've tried everything but can't seem to get Part B. I must be missing something. This is one of those online assignments where you get as many attempts as you want. I keep getting Part A, but can't get Part B. Please explain how you did Part B if you get it. I have the correct answers too.
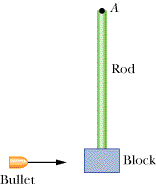
In Fig. 11-52, a 7.3 g bullet is fired into a 0.46 kg block attached to the end of a 0.12 m nonuniform rod of mass 0.88 kg. The block-rod-bullet system then rotates in the plane of the figure, about a fixed axis at A. The rotational inertia of the rod alone about A is 0.038 kg·m2. Treat the block as a particle. (a) What then is the rotational inertia of the block-rod-bullet system about point A? (b) If the angular speed of the system about A just after impact is 7.2 rad/s, what is the bullet's speed just before impact?