Baez and Perez beef strings and branes

[marcus]

this just appeared today
http://arxiv.org/abs/gr-qc/0605087
Quantization of strings and branes coupled to BF theory
John C. Baez, Alejandro Perez
"BF theory is a topological theory that can be seen as a natural generalization of 3-dimensional gravity to arbitrary dimensions. Here we show that the coupling to point particles that is natural in three dimensions generalizes in a direct way to BF theory in d dimensions coupled to (d-3)-branes. In the resulting model, the connection is flat except along the membrane world-sheet, where it has a conical singularity whose strength is proportional to the membrane tension. As a step towards canonically quantizing these models, we show that a basis of kinematical states is given by 'membrane spin networks', which are spin networks equipped with extra data where their edges end on a brane."

 

[marcus]

I am embarrassed to say that I don't at all understand the motivation of this paper or where it could be heading.
I would welcome insights anybody has to offer that would connect it up with the other recent Baez paper, which is this paper's reference [5]

[5] Exotic statistics for loops in 4d BF theory
http://arxiv.org/gr-qc/0603085

the last paragraph of the conclusions of the Baez Perez article is a bit vague and I do not get a definite notion of what they think is possible along these lines:

"It will be interesting to carry out the study of four-dimensional BF theory coupled to strings in analogy to what has already been done for three-dimensional gravity coupled to point particles. For example, point particles in three-dimensional gravity are known to obey exotic statistics governed by the braid group. Similarly, we have argued in the companion to this paper that strings coupled to four-dimensional BF theory obey exotic statistics governed by the ‘loop braid group’ [5]. In that paper we studied these statistics in detail for the case G = SO(3, 1), but we treated the strings merely as gauge defects. It would be good to study this issue more carefully with the help of the framework developed here."

It sounds like they are proposing to re-examine the 4D case of beef that they studied in ref [5], with this new framework (which I'm not sure what it is)------and in reference [5] they got a bunch of particles with curious statistics. Presumably by re-studying with a new framework they will get a different bunch of particles. Maybe it will have some resemblance to those in nature---or a significant feature will offer clue to how one might

get the standard rabbit of particles to jump
out of the hat of gravity.

If that is what Baez has in mind then he is sure holding his cards close to his vest, because I don't get any clear signals from what they actually wrote in their conclusions.

If I remember correctly what Baez said a few days ago in TWF, he is currently visiting at Perimeter

 

[marcus]

should put a link to the earlier thread about the Baez Wise Crans article
https://www.physicsforums.com/showthread.php?t=115082

Derek Wise just posted on that thread to explain why they changed the title of the paper----which is now clear.

loops have a vertex (a spot they go around and come back to)

if you erase the vertex then it's different and needs to be called something else----like for example a "string"

a closed "string" is a loop with no distinguished basepoint

 

[selfAdjoint]

Marcus, maybe your bafflement at where Baez is going is because you're thinking like a physicist - "what is the physical meaning of all this?" - while Baez is thinking like a mathematician - "Isn't this fascinating? And look how it links up to this other thing over here!".

Physicists trying to grok Witten have the same problem.

 

[marcus]

Marcus, maybe your bafflement at where Baez is going is because you're thinking like a physicist - "what is the physical meaning of all this?" - while Baez is thinking like a mathematician - "Isn't this fascinating? And look how it links up to this other thing over here!".

Physicists trying to grok Witten have the same problem.

kind of you to put such a nice face on it but in this case my predicament is probabably worse: at this point I am simply trying to understand it as a science-watching member of the public----even though I guess I could try to view it from the mathematician's side as well (isnt this neat, could it be the tip of a big theorem?)---at least yesterday i had a mustardseed of faith that it would somehow reveal physical meaning once they got it right.

 

[arivero]

like a physicist - "what is the physical meaning of all this?" - (...)
like a mathematician - "Isn't this fascinating? And look how it links up to this other thing over here!".

I like to call this the Botanist/physicist duality, more than math/phys, because mathematicians really go over both phases: they research the forest locating and labeling new objects, and then they go for a classification theorem or a generative formula explaining their "meaning".

 

[f-h]

It certainly could mean something. In the big picture I think it's just one of many leads that can be investigated.

Point particles(worldlines) are natural in 2+1 Gravity, Strings (worldsheets) in 3+1 membranes in higher dimensions. As was pointed out to me today that's simply because you want to break topological invariance which is enforced by the B field, which because curvature is a 2-form is a codimension 2-form which naturally "couples to the defects".

matter as defects in toplogical theory is what freidel has been doing, so this is the start of a possible generalization of his work to 4d. (all IMHO)

 

[marcus]

matter as defects in toplogical theory is what freidel has been doing, so this is the start of a possible generalization of his work to 4d. (all IMHO)

Jeez, you mean that Baez is pitching in and getting behind Freidel's effort!?

if that is really what is behind it that is wonderful.
maybe we should all hold our breath and not say anything for a few minutes, like when you blow out the candles you should not tell anyone your wish

 

[f-h]

Marcus, I have as much knowledge as you on Baez's intentions. Topological defects as particles precedes Freidel as well by quite a bit, all I'm saying that this is an approach to matter relevant to LQG in the widest sense, and in this wide context Baez/Perez have developed a very natural generalization to arbitrary dimensions. That's all.Baez has talked tangentially about strings and spinfoams before:

http://arxiv.org/abs/quant-ph/0404040

"There is not one whit of experimental evidence for either string theory or loop quantum gravity,
and both theories have some serious problems, so it might seem premature for philosophers to
consider their implications. It indeed makes little sense for philosophers to spend time chasing every
short-lived fad in these fast-moving subjects. Instead, what is worthy of reflection is that these two
approaches to quantum gravity, while disagreeing heatedly on so many issues [32, 33], have so much
in common. It suggests that in our attempts to reconcile the quantum-theoretic notions of state and
process with the relativistic notions of space and spacetime, we have a limited supply of promising
ideas. It is an open question whether these ideas will be up to the task of describing nature."

BUT that was a philosophical "let's talk" paper as opposed to this very technical result here, so (as always) the parallel of words should not be taken to automatically imply a topical connection.

 

[marcus]

Baez has talked tangentially about strings and spinfoams before:

http://arxiv.org/abs/quant-ph/0404040

...

I remember when Baez posted fortyfortyforty.
It is a charming paper. the idea of a star-category is nice and easy to understand too.

Well, for now we wait.

I am in suspense about how Freidel is coming with the 4D case.

Not a propos of this or anything else especially, I wish Danny Terno would speak up.

 

[f-h]

The news from the front is that this is (just) a natural model to play with, without an immediate physical interpretation. selfAdjoint is spot on I think.

Potentially it could connect to (elementary) String theory. For now the model is rich enough that there are potential projects for quite a while to come from this starting point.

 

[john baez]

quantization of strings and branes coupled to BF theory

I am embarrassed to say that I don't at all understand the motivation of this paper or where it could be heading.

Don't be embarrassed; we mainly just wanted to get the paper out, and wait 'til later before expanding on where we're going with it.

I would welcome insights anybody has to offer that would connect it up with the other recent Baez paper, which is this paper's reference [5]:

http://arxiv.org/abs/gr-qc/0603085"

You're right to mention this other paper, because it's about the exact same subject: getting matter to arise naturally from topological gravity in 4 dimensions, just as it does from gravity in 3 dimensions.

In short, we're trying to realize John Wheeler's old "matter without matter" idea, where one seeks to:

get the standard rabbit of particles to jump out of the hat of gravity.

But, the cool part is that while 3d gravity naturally gives birth to point particles, 4d topological gravity naturally gives birth to strings.

I will explain how it all works in "http://math.ucr.edu/home/baez/week232.html" " of This Week's Finds. (Don't click on link this until, oh, say, May 20th, since I'm not done writing it yet.)

The main reason I don't want to sing, dance and philosophize about this stuff too much is that we're taking ideas from 3d gravity and generalizing them, not to 4d gravity (which nobody understands), but 4d topological gravity (also known as BF theory). So, in a sense it's just a mathematical exercise. But, it's so beautiful that anybody who finds 3d gravity interesting should find this interesting too. We get all the same effects: exotic statistics, doubly special relativity, and so on...

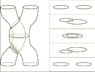
But, the simple-minded method that gives point particles in 3d gravity - just cut out little discs from your 2d space, and they act like particles - turns out to gives strings in 4d topological gravity - now cut out solid tori!

If that is what Baez has in mind then he is sure holding his cards close to his vest, because I don't get any clear signals from what they actually wrote in their conclusions.

It sounds like you understood the point exactly. In the paper with Crans and Wise, we worked out how strings in 4d BF theory would have "exotic statistics" - neither fermions nor bosons, but something more complicated. In the paper with Perez, we wrote down a Lagrangian for strings in 4d BF theory, so one can actually study their dynamics. And then we described a way to quantize the resulting theory using spin networks. The picture in the paper says it all.

If I remember correctly what Baez said a few days ago in TWF, he is currently visiting at Perimeter.

Yeah, I came to the Perimeter Institute on Monday, and tomorrow I'm going to give this talk:


Strings Coupled to BF Theory in 4 Dimensions


Quantum gravity in 3 dimensions can be described by BF
theory, which is a purely topological theory. While
this theory was exactly solved in the 1980s by Witten,
Turaev and Viro, it revealed a new layer of depth when
point particles with their usual dynamics were seen to
arise naturally as "topological defects": world-lines
along which the gauge field is singular. Here we describe
how the same mechanism yields string-like excitations in
4d BF theory. Just as point particles in 3d BF theory have
exotic statistics governed by the braid group, these strings
have statistics governed by the loop braid group. Also,
just as Wilson loop observables are important in 3d BF
theory, "Wilson surface" observables arise naturally from
treating 4d BF theory as a higher gauge theory.

Unfortunately I won't have any transparencies for you to see, since I'm in a big rush preparing it, so I'll give a blackboard talk.

But, on May 31st I'll give the weekly colloquium, and I should have some transparencies by then, and they may even videotape me. A seemingly different topic, but actually just part of the same project:

http://math.ucr.edu/home/baez/quantum_spacetime"

Category theory is a general language for describing things and
processes - called "objects" and "morphisms". In this language,
the counterintuitive features of quantum theory turn out to be
properties that the category of Hilbert spaces shares with the
category of cobordisms - in which objects are choices of "space",
and morphisms are choices of "spacetime". The striking similarities
between these categories suggests that "n-categories with duals"
are a promising framework for a quantum theory of spacetime.
We sketch the historical development of these ideas from Feynman
diagrams, to string theory, topological quantum field theory, spin
networks and spin foams, and especially recent work on open-closed
string theory, quantum gravity coupled to point particles, and 4d
BF theory coupled to strings.

 

[john baez]

Jeez, you mean that Baez is pitching in and getting behind Freidel's effort!?

Yes, I came to the Perimeter Institute precisely to talk to him, because he's doing the coolest stuff with spin foams. It's nice to hear that you care.

My two quantum gravity students, Jeff Morton and Derek Wise, will come out here later. They are doing theses closely related to Laurent Freidel's work. Personally I'd be very happy doing just math, but having students who want to work on physics, I feel a kind of obligation to keep my finger in the pot - which means figuring out what Laurent is up to and helping him do it.

if that is really what is behind it that is wonderful.
maybe we should all hold our breath and not say anything for a few minutes, like when you blow out the candles you should not tell anyone your wish

Wow, that's very kind of you.

Since you seem interested: I showed up on Monday and spent this morning having my first serious talk with Laurent. As you probably know, he has figured out how to express ordinary Feynman diagram calculations in 3d quantum field theory in terms of a spin foam model, and then he can "turn on gravity" in this theory and do calculations involving point particles coupled to 3d quantum gravity. It's all very precise and beautiful.

Now he is writing a bunch of papers which seek to extend these results to 4 dimensions. In fact he's writing 3 papers with Artem Starodubtsev and one with Aristide Baratin. So far, one thing they know how to do is express ordinary Feynman diagrams in 4d quantum gravity in terms of a spin foam model. The obvious next step would be to "turn on gravity". But it's not so obvious how to do this - in part because the spin foam model they already have is somewhat mysterious: it's not like any known one. He and I both believe that understanding it will require some help from higher category theory. That's where I come in.

So, basically I'm learning about his work, teaching him about 2-groups and their representations, and we're trying to see if his spin foam model is related to this sort of math. It's actually incredibly exciting to me - because even if the connection to quantum gravity never pans out, it seems to be revealing some higher category theory lurking in the structure of ordinary quantum field theory.

Since I think higher categories (n-categories) are lurking everywhere, just waiting to be seen and understood, this sort of possibility is right up my alley.

 

[Careful]

**theory would have "exotic statistics" - neither fermions nor bosons, but something more complicated. In the paper with Perez, we wrote down a Lagrangian for strings in 4d BF theory, so one can actually study their dynamics. And then we described a way to quantize the resulting theory using spin networks. The picture in the paper says it all.
**

Just a few small questions. The only quantum gravity statistics I know of is the one developped by Surya, Sorkin and Balachandran in the canonical formulation for the wave function of the universe (so I did not read your paper). In formulating quantum statistics for any configuration degrees of freedom whatsoever, it is important to tell in what sense they are indistinguishable and what an interchange means. In the context of the latter approach, this implies that you need a background spatial topology (R^3) as well as the fact that the topological geons are not distinguishable from the *metrical* point of view (quasi indentical geons were matched to almost Euclidean space in this construction AFAIR). So, (a) how does this construction relate to yours ? (b) how do you adress the previously mentioned issues within this paper?

Cheers,

Careful

 

[john baez]

Point particles(worldlines) are natural in 2+1 gravity, strings (worldsheets) in 3+1, membranes in higher dimensions. As was pointed out to me today that's simply because you want to break topological invariance which is enforced by the B field, which because curvature is a 2-form is a codimension 2-form which naturally "couples to the defects".

Exactly - you got it.

matter as defects in toplogical theory is what freidel has been doing, so this is the start of a possible generalization of his work to 4d. (all IMHO)

That's the plan... we're not trying to keep it secret, although I suppose we're not eager to explain all the things we hope we can do eventually - better to sell the product when it actually exists.

Here's what we said in the first paragraph of our paper:

Interest in the quantization of 2+1 gravity coupled to point
particles has been revived in the context of the spin foam
and loop quantum gravity approaches to the nonperturbative
and background-independent quantization of gravity. On the
one hand this simple system provides a nontrivial example where
the strict relation between the covariant and canonical approaches
can be demonstrated. On the other hand intriguing relationships
with field theories with infinitely many degrees of freedom have
been obtained.

The idea of generalizing this construction to higher dimensions is
very appealing. We will argue that in 3+1 dimensions, the natural
objects replacing point particles are strings. This idea has already
been studied in a companion paper, which treated these strings merely
as defects in the gauge field---i.e., places where it has a conical
singularity. Here we propose a specific dynamics for the theory and
a strategy for quantizing it. More generally, in d-dimensional spacetime
we describe a way to couple (d-3)-branes to BF theory.

I suppose this has too much jargon to be really clear. For example, Alejandro wanted to emphasize that 3d quantum gravity

provides a nontrivial example where
the strict relation between the covariant and
canonical approaches can be demonstrated

because he just wrote a wonderful paper where he proved rigorously that the spin foam model of quantum gravity in 3 dimensions gives results that match loop quantum gravity. People thought this would be true, but it's nice to know it's true.

Similarly,

On the other hand intriguing relationships
with field theories with infinitely many degrees
of freedom have been obtained.

is a highly academic way of saying "it's incredibly cool that 3d quantum gravity reduces to ordinary quantum field theory when you let the gravitational constant approach zero!" Again, there's a reference to the relevant work (which I've deleted here).

 

[john baez]

Just a few small questions. The only quantum gravity statistics I know of is the one developped by Surya, Sorkin and Balachandran in the canonical formulation for the wave function of the universe...

Right. We're actually working with "topological gravity", aka BF theory, but a lot of the underlying issues are the same. In fact, we cite papers by Balachandran, Surya and others on exotic statistics for strings - there's been work on this kind of thing before, just not quite the same.

In formulating quantum statistics for any configuration degrees of freedom whatsoever, it is important to tell in what sense they are indistinguishable and what an interchange means. In the context of the latter approach, this implies that you need a background spatial topology (R^3) ...

Yes, in our paper the topology of space is R^3. We could do stuff for fancier topologies, but we're already having enough fun...

as well as the fact that the topological geons are not distinguishable from the *metrical* point of view (quasi indentical geons were matched to almost Euclidean space in this construction AFAIR).

We've got a flat connection on R^3 with a bunch of circles removed - that's what BF theory gives us - and we see how the connection changes when we move the circles around. We can exchange them either by moving them around each other, or through each other, so the statistics are governed by a group called the "loop braid group" or "braid permutation group".

http://arxiv.org/abs/gr-qc/0603085" is packed with beautiful pictures, and it has a gentle expository introduction, so I really urge you to take a look... you'll probably get the idea without needing to read it carefully, given that you've seen that topological geon stuff.

I actually ran into Sorkin on the street in Chicago last week, completely out of the blue - he was visiting his mother!

 

[Careful]

**
I actually ran into Sorkin on the street in Chicago last week, completely out of the blue - he was visiting his mother! **

Nice, did not see Rafael for a long time. But coming a bit back to the topological field theory (I did not pay much attention to that given that gravitation isn't topological) : I guess the reason you can do this is because BF theory does give a unique vacuum, right ? And I guess the idea would be that you try to put the gravitational waves on this ? I say this because you would expect the statistics only to hold approximately in the latter case (in the weak field limit !).

Careful

 

[marcus]

I just got back and checked in. This discussion with Baez is great!

 

[john baez]

Nice, did not see Rafael for a long time.

Ah, so you used to work with him or something? I see him at conferences here and there; for example, he and Surya were at Loops '05. He's a nice guy - and amazingly resistant to following other people's trends!

But coming a bit back to the topological field theory (I did not pay much attention to that given that gravitation isn't topological) : I guess the reason you can do this is because BF theory does give a unique vacuum, right?

For me, the term "vacuum" means something like "lowest-energy eigenstate of the Hamiltonian", so this concept makes sense in ordinary quantum field theory on Minkowski spacetime, for example, but not in the context of gravity or topological quantum field theory - at least, not without further explanation.

BF theory has a unique solution (up to gauge transformations) on R^4, so one could say it has a unique vacuum if one wanted, but that would be insufficiently forceful - it actually has a unique state. Not just one way for nothing to be, but one way for anything to be.

However, we get around this by cutting little circles out of space - let's call them "strings", because that's sort of how they act. Classically there are lots of solutions of BF theory on R^4 with the worldsheets of these strings removed; it turns out these solutions are characterized by assigning a kind of "momentum" to each string. And, quantum-mechanically too, we get a big Hilbert space of states, which is a tensor product of state spaces for each string.

The "loop braid group" describes all the ways we can move these strings around or through each other. It's an interesting blend of the permutation group and the braid group. And, it acts on Hilbert space of states. This action describes the "statistics" of our strings. They act like bosons when we move one around another, but in a more interesting way when we move one through another.

And I guess the idea would be that you try to put the gravitational waves on this ? I say this because you would expect the statistics only to hold approximately in the latter case (in the weak field limit!).

I guess so - but this is not my main interest right now. I'm just studying this theory for what it is. My idea is that if people are willing to spend years studying 3d quantum gravity, which is a purely topological theory without any gravitational waves, but still shockingly deep (exotic statistics, doubly special relativity, matter without matter), it's probably worth thinking a bit about a 4d theory with all the same properties but where strings replace point particles. For example, I want to see if these strings we're getting give an example of a topological string theory in the formal sense.

Of course, what Freidel and Starodubtsev are doing is treating 4d gravity as a perturbation around 4d BF theory. If that works, the stuff I'm doing will be like investigating free quantum field theory - a good thing to do, if you're going to build an interacting quantum field theory on top of it!

So then, yeah, I guess the statistics get more complicated.

 

[Careful]

** He's a nice guy - and amazingly resistant to following other people's trends! **

He is, but his stubornness is a transferrable desease, be aware of that !


**
BF theory has a unique solution (up to gauge transformations) on R^4, so one could say it has a unique vacuum if one wanted, but that would be insufficiently forceful - it actually has a unique state. Not just one way for nothing to be, but one way for anything to be. **

Well I guess that the solutions of BF theory are associated with the second cohomology classes of spacetime (the true fundamental degrees of freedom of the theory?) and likewise are the states which would explain your statement. The description you give to the loop braid group sounds familiar from Surya et al.


Cheers,

Careful

 

[ccdantas]

Excellent to read these clarifying posts by John Baez.

BTW, any idea when the 2nd edition of Gauge Fields, Knots, and Gravity will be available?

Best wishes
Christine

 

[john baez]

BTW, any idea when the 2nd edition of Gauge Fields, Knots, and Gravity will be available?

They told me that they're sending me a copy, so it should be available pretty soon.

In fact, when I just went to the https://www.worldscibooks.com/physics/2324.html" website, they seemed willing to sell me one. Maybe you can try to buy one, and let me know if it works or not?

By the way, it's not officiallly called a "2nd edition". However, all the typos that I knew about should be corrected. For example, the wonderful quote by Maxwell which was missing at the end of the book should now be there. But, given how the world works, they have probably inserted some equally horrible new flaw.

 

[john baez]

Well I guess that the solutions of BF theory are associated with the second cohomology classes of spacetime (the true fundamental degrees of freedom of the theory?) and likewise are the states which would explain your statement.

It's not second cohomology...

 

[john baez]

http://arxiv.org/abs/gr-qc/0603085" is packed with beautiful pictures...

Let me try to attach one of those pictures using the file attachment option... I've never tried this before, so we'll see how it goes. This is supposed to be a "movie" illustrating how one string braids around another:

pretty picture

 

[john baez]

Let me try to attach one of those pictures using the file attachment option... I've never tried this before, so we'll see how it goes.

Looks like it worked, but looks like I both attached a picture and attached a link to it... a bit redundant. Just to check, let me try attaching another picture, without attaching the link.

This is about exotic statistics in 3d quantum gravity. Space is a plane. As we move one particle around another on the plane, they trace out braid in spacetime. We carry Wilson loops around in the process - the red curves in this picture. These can tell whether we braid the particles around clockwise or counterclockwise!

 

[marcus]

key pictures from the new papers.
fresh mathematics arriving like takeout
in my livingroom courtesy of the internet
which quietly whispers "eureka".
delighted by these posts.

 

[Careful]

It's not second cohomology...

I am just curious to know what it is then, as I said, never looked upon BF theory.

Cheers,

Careful

 

[john baez]

I am just curious to know what it is then, as I said, never looked upon BF theory.

Okay. I'll talk about BF theory with vanishing cosmological constant,
with Lagrangian tr(B ^ F). This makes sense in spacetime of any dimension n, with A a connection, F its curvature, and B a Lie-algebra-valued (n-2)-form.

Suppose "space" is some (n-1)-manifold S. Then the classical configuration space for BF theory is the space of flat connections mod gauge transformations on S - the so-called "moduli space of flat connections". The quantum Hilbert space is L^2 of this.

For a lot of fun stuff on BF theory in 3 and 4 dimensions, probably less stressful than the above paragraphs , folks can now read http://math.ucr.edu/home/baez/week232.html" of This Week's Finds. More pretty pictures!

 

[Careful]

Okay. I'll talk about BF theory with vanishing cosmological constant,
with Lagrangian tr(B ^ F). This makes sense in spacetime of any dimension n, with A a connection, F its curvature, and B a Lie-algebra-valued (n-2)-form.

Suppose "space" is some (n-1)-manifold S. Then the classical configuration space for BF theory is the space of flat connections mod gauge transformations on S - the so-called "moduli space of flat connections". The quantum Hilbert space is L^2 of this.

For a lot of fun stuff on BF theory in 3 and 4 dimensions, probably less stressful than the above paragraphs , folks can now read http://math.ucr.edu/home/baez/week232.html" of This Week's Finds. More pretty pictures!

I was probing for a classification of the flat connections, ie. the moduli space (in which the cohomology groups of the underlying spacetime are important, but obviously not sufficient). I know of the classification in two spatial dimensions (where you basically have 6g - 6 moduli for g > 1 and 2 for g=1, g is the genus) - here the first homotopy (or the fundamental) group of space is obviously important. However, I never upgraded my knowledge to three spatial dimensions (where you need the work of Thurston I presume). So basically, my question was about the importance of the latter work for quantization of 3+1 dimensional BF theory (and to what extend it is used already).

On R^3, there is only one flat connection (modulo gauge transformations) -> one dimensional quantum theory = one state (which is what John Baez said in post 19). I guess it is justified to call this the vacuum state since no particles, in the form of topological defects, are present.

 

[john baez]

moduli space of flat connections

I was probing for a classification of the flat connections, ie. the moduli space (in which the cohomology groups of the underlying spacetime are important, but obviously not sufficient).

Okay!

The easiest thing to describe is the "moduli space of flat G-bundles" over any connected manifold M. Points in this are gauge equivalence classes of G-bundles with flat connection over M. This space turns out to be

hom(pi_1(M), G)/G

where pi_1(M) is the fundamental group of M, hom(pi_1(M), G) is the space of homomorphisms from this fundamental group to G, and G acts on this by conjugation. It's pretty easy to see that any G-bundle with connection over M gives a point in this space: just consider the holonomies of Wilson loops. The slightly harder part is to see that any point in this space comes from a flat connection on some G-bundle over M.

Typically the moduli space of flat G-bundles over M is a union of pieces corresponding to different G-bundles. These pieces are called "moduli spaces of flat connections".

When G is U(1),

hom(pi_1(M), G)/G = hom(H_1(M), U(1))

You can find explanations of this stuff in my http://math.ucr.edu/home/baez/qg-winter2005/" the stuff they needed to start work on their thesis projects.

 

[Careful]

**
The easiest thing to describe is the "moduli space of flat G-bundles" over any connected manifold M. Points in this are gauge equivalence classes of G-bundles with flat connection over M. This space turns out to be **


Thanks for providing this information which will allow many people here to better understand the context in which to see this work.

Cheers,

Careful

 

[marcus]

...

Thanks for providing this information which will allow many people here to better understand the context in which to understand this work.
...

Compliments on your side as well, Mr. Careful.

 

[Careful]

Compliments on your side as well, Mr. Careful.

Well, I must confess I passively knew this classification result but it got kind of in some more distant part of my memory. Hence, it was useful for me too in that respect (and nothing is better than an explanation by a good mathematical physicist who is actively doing this particular stuff).

 

[Mike2]

Category theory is a general language for describing things and
processes - called "objects" and "morphisms". In this language,
the counterintuitive features of quantum theory turn out to be
properties that the category of Hilbert spaces shares with the
category of cobordisms - in which objects are choices of "space",
and morphisms are choices of "spacetime". The striking similarities
between these categories suggests that "n-categories with duals"
are a promising framework for a quantum theory of spacetime.
We sketch the historical development of these ideas from Feynman
diagrams, to string theory, topological quantum field theory, spin
networks and spin foams, and especially recent work on open-closed
string theory, quantum gravity coupled to point particles, and 4d
BF theory coupled to strings.

I wonder if there is an merit to the idea of a category where the objects ARE the morphisms. I'm thinking that in the very very early universe, when the universe was just a single particle (?), was the universe then an object or a process? Perhaps the two were indistinguishable at that point. I'm also thinking in terms of QCD where the particles (objects?) that give rise to the forces (processes?) are indistinquishable, the force carrier is the same as the particle being forced, IIRC. Any thoughts along these lines? Would this be the "dual" that you mention above? Thanks.

 

[Kea]

I wonder if there is any merit to the idea of a category where the objects ARE the morphisms.

Actually, objects are really identity arrows, so everything is a morphism. The correspondence you propose, however, is too simplistic. Physically, an origin to a classical universe must be a complex entity - a morphism, sure, like everything, but one needs to understand exactly what kind, and this is not a simple question.

The duals might be dual Hilbert spaces, in the usual sense, or at a much deeper level, String type duals.