kinghong1970
- 1
- 0
Hi guys,
great forum you have here...
basically, a couple of years ago, I've gotten involved in the hobby of watercooling computers by adding a radiator, pump and waterblocks on the cpus and other heat sources.
well, as I've been researching builds by other folks, i notice that some folks put fans on their radiators in various methods...
i just have some questions that perhaps you guys can help with...
120mm Fans:
Stacked Push:

Stacked Pull:

Push Pull:

140mm Fans + 40mm Tapered Shroud
Stacked Push
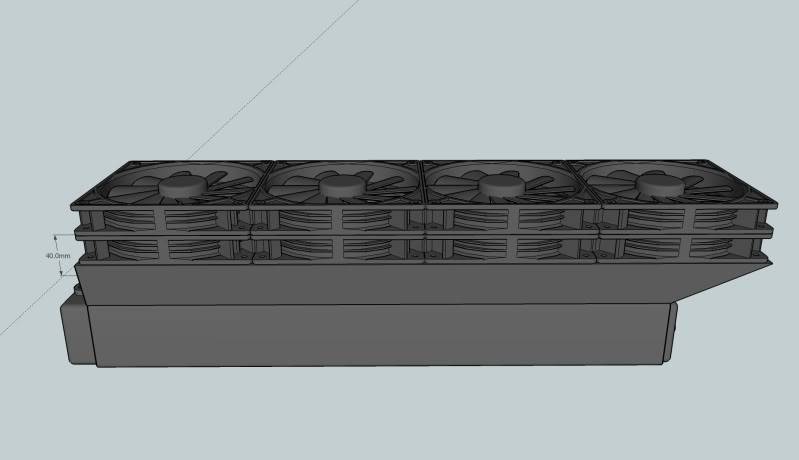
Stacked Pull
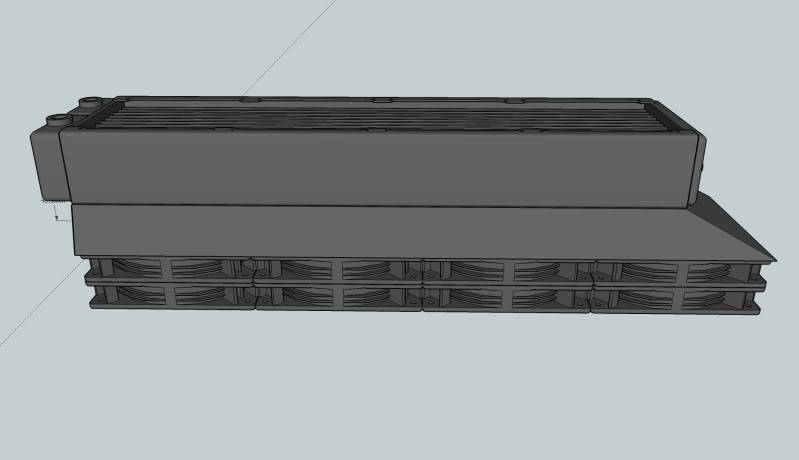
the fans used quite commonly are:
120mm Yate Loon
Model: D12SM-12
Fan Size: 120mm x 120mm x 25mm
Speed: 1650 +/- 10% RPM
Airflow: 70.5 CFM
Noise: 33.0 dBA
Bearing: Sleeve
Voltage: 12 V
Current: .3 Amp Max
Fan Life: 30,000 hours
Connector: 3pin and 4pin pass-through connector
140mm Yate Loon
Model: D14SM-12
Fan Size: 140mm x 140mm x 25mm
Speed: 1400 +/- 10% RPM
Airflow: 62 CFM
Noise: 29.0 dBA
Bearing: Sleeve
Voltage: 12 V
Current: .7 Amp Max
Connector: 3pin and 4pin pass-through connector
1) now, in the 120mm fan arrangements, what would be the better fan arrangement of choice to improve the performance of the radiator?
2) in the 140mm fan arrangements, will there be an improvement over 120mm fan in similar arrangements, say stacked push 120mm vs stacked push 140mm?
3) with the 140mm fans, which would be perfered choice of arrangements to improve radiator performance?
4) is there an advantage of using 140mm fans to feed a 120mm fan sized radiator?
i hope that this was not inappropriate for this forum...
thanks in advance.
great forum you have here...
basically, a couple of years ago, I've gotten involved in the hobby of watercooling computers by adding a radiator, pump and waterblocks on the cpus and other heat sources.
well, as I've been researching builds by other folks, i notice that some folks put fans on their radiators in various methods...
i just have some questions that perhaps you guys can help with...
120mm Fans:
Stacked Push:
Stacked Pull:
Push Pull:
140mm Fans + 40mm Tapered Shroud
Stacked Push
Stacked Pull
the fans used quite commonly are:
120mm Yate Loon
Model: D12SM-12
Fan Size: 120mm x 120mm x 25mm
Speed: 1650 +/- 10% RPM
Airflow: 70.5 CFM
Noise: 33.0 dBA
Bearing: Sleeve
Voltage: 12 V
Current: .3 Amp Max
Fan Life: 30,000 hours
Connector: 3pin and 4pin pass-through connector
140mm Yate Loon
Model: D14SM-12
Fan Size: 140mm x 140mm x 25mm
Speed: 1400 +/- 10% RPM
Airflow: 62 CFM
Noise: 29.0 dBA
Bearing: Sleeve
Voltage: 12 V
Current: .7 Amp Max
Connector: 3pin and 4pin pass-through connector
1) now, in the 120mm fan arrangements, what would be the better fan arrangement of choice to improve the performance of the radiator?
2) in the 140mm fan arrangements, will there be an improvement over 120mm fan in similar arrangements, say stacked push 120mm vs stacked push 140mm?
3) with the 140mm fans, which would be perfered choice of arrangements to improve radiator performance?
4) is there an advantage of using 140mm fans to feed a 120mm fan sized radiator?
i hope that this was not inappropriate for this forum...
thanks in advance.