Gimbaled Gyroscope: Do I Need Constant Torque?

[Viroos]

Hi !
I have very basic question about gyroscopes: do I need same torque from gimbal motor to accelerate the flywheel whenever it's rotating or not ? (and the gimbal motor is attached to the floor)

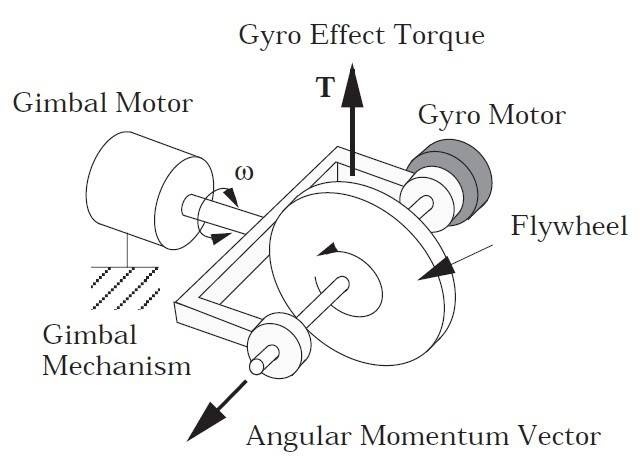
Thanks in advance :)

 

[Viroos]

Anybody ?

 

[vin300]

The torque applied from the gimbal motor is not going to accelerate it, it is only going to cause precessional motion at a particular constant angular velocity. You'd have to change the torque to change the velocity of precession. The couple is equal to moment of inertia times the cross product of velocity of precession and vel. of spin.
There's something wrong with your diagram. The input couple causes precession about a perpendicular axis but this kind of motion is not possible from what is seen in the drawing.

 

[Viroos]

That's what is confusing me-the gimbal motor is fixed to the floor, so the precession is impossible and the only possible rotation is "omega", and that's exactly the problem-is there any difference in the gimbal motor torque when the flywheel is rotating and when it's not ?

 

[vin300]

The same amount of torque will be required to accelerate the flywheel irrespective of whether it's rotating or not, but the gyroscopic couple will produce bending moment of the gimbal shaft.