How Does a Positron Behave in a Penning Trap?

[stunner5000pt]

Please help! Penning TRAPP!

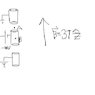
A Penning trap is described as in the attachment labelled Penn

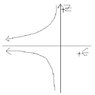
Sketc the heelctric field - CHeck out the other attachment

Describe motion of positron if released from point A - osillate from top cylinder to top edge of bottom cylinder back and forth??

Describe motion of positron if released from B with small 1eV kinetic energy in +Z direction
Just like the previous part??

If released from point B with 1eV kinetic energy in +X direction
WIll collide with both sides of the electrode??

Please tell me if i wrong with any of these i really need help with electricity!

 

[Nate810]

Yes, the motion of a positron released from point B with 1eV kinetic energy in +X direction will collide with both sides of the electrode. However, the direction of motion can be altered due to the electric field and magnetic field within the trap, so it may not necessarily just move in a straight line.

 

[wais]

Sure, I'd be happy to help with understanding the Penning trap and the motion of a positron within it.

First, let's clarify what a Penning trap is. It is a type of particle trap that uses electric and magnetic fields to confine charged particles, such as positrons, in a specific region. This allows for the study of the particles' characteristics and behavior.

Now, let's address the specific questions you have asked. In the attachment labeled "Penn", a schematic of a Penning trap is shown. As you can see, it consists of a central electrode, a cylindrical outer electrode, and a magnetic field. The electric field is produced by applying a voltage difference between the central electrode and the outer electrode.

When a positron is released from point A, it will experience a force due to the electric and magnetic fields. This will cause it to oscillate between the top cylinder and the top edge of the bottom cylinder, as you mentioned. This motion is known as a cyclotron motion.

If the positron is released from point B with a small 1eV kinetic energy in the +Z direction, it will also experience a cyclotron motion, but it will be confined to the +Z direction due to its initial kinetic energy. It will still oscillate between the top and bottom cylinders, but its motion will be more restricted.

Similarly, if the positron is released from point B with 1eV kinetic energy in the +X direction, it will experience a cyclotron motion, but this time it will be confined to the +X direction. It will collide with both sides of the electrode as it oscillates back and forth.

I hope this helps clarify the motion of a positron in a Penning trap. If you have any other questions or need further clarification, please don't hesitate to ask. Best of luck with your studies!