How to calculate the magnetic field and pull force generated by current?!

Momento

Hallo all,


I've been looking around to find the best way to calculate the magnetic field generated by current flowing through copper wire... There were many sites I've found but its kinda confusing

One of the laws:

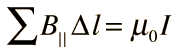
I thought it was simple to determine the magnetic field... Is there a way to calculate the pull force as well?!

Thanks in advance!

Nessdude14

The strength of the magnetic field around a long, straight wire is:
[itex]\Large B=\frac{μ_{0}I}{2\pi r}[/itex]
B is the magnetic field in Tesla, μ₀ is the permeability constant (1.26*10^-6 T m/A), I is current in Amps, and r is distance from the wire in meters.
The direction of the field is given by the following "right-hand rule":


When you want to calculate for a wire that's not perfectly straight, this equation isn't valid, and you must use integration to account for an odd-shaped wire.

Momento

Thank you so much for that!

I'm looking up for more equations because most probably I'll make a series of looped wires and tie the together...