boeing_737
- 8
- 0
Hi,
I am having a little bit of conceptual trouble with this problem and would appreciate your help. The problem setup is given in the figure. Let's say we have a slender uniform rigid arm(mass m, length l) in space, with a coordinate system B attached to the left end of the arm as shown. C is the center of mass of the arm. We have a moment M_{z_b} acting about the \hat{z}_{b} axis.
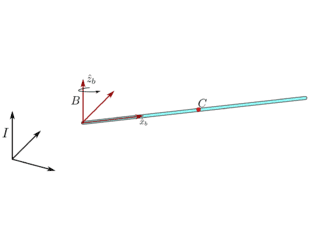
Let (u,v,w) and (p,q,r) be the inertial velocity and inertial angular velocity vectors expressed in B. I get the scalar equations of motion as (assuming that the angular velocity is only along \hat{z}_b):
m \dot{u} - \frac{ml}{2} r^2 = F_{x_b}
m \dot{v} + \frac{ml}{2} \dot{r} = F_{y_b}
m \dot{w} = F_{z_b}
0 = M_{x_b}
-\frac{ml}{2} \dot{w} = M_{y_b}
\frac{ml^2}{3} \dot{r} + \frac{ml}{2} \dot{v} = M_{z_b}
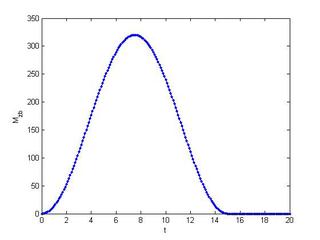
The applied moment is given as : M_{z_b}(t) = 160 \left(1 - \cos \left(\frac{2 \pi t}{15} \right) \right). For t > 15, M_{z_b} = 0. See figure below :
Integrating these equations using MATLAB's ode45, I get the following plot :
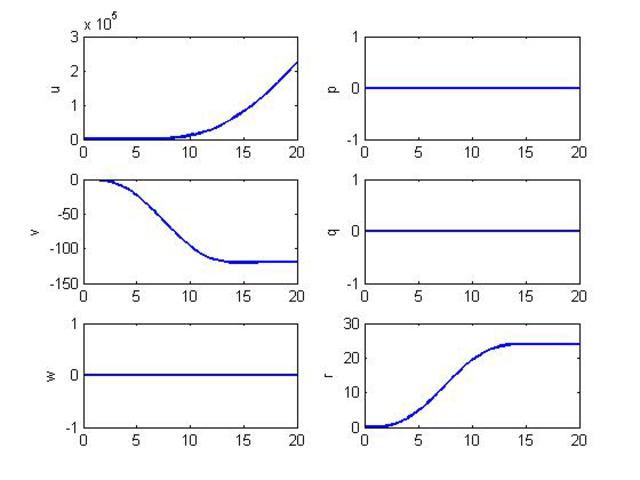
From the above figure :
1) There is only one component of angular velocity (yaw rate) which is as expected. But is the magnitude correct (ie should it reach 24 rad/s)?
2) I am not able to figure out what's going on with u. Why is it increasing so rapidly?
Any help would be really appreciated.
yogesh
I am having a little bit of conceptual trouble with this problem and would appreciate your help. The problem setup is given in the figure. Let's say we have a slender uniform rigid arm(mass m, length l) in space, with a coordinate system B attached to the left end of the arm as shown. C is the center of mass of the arm. We have a moment M_{z_b} acting about the \hat{z}_{b} axis.
Let (u,v,w) and (p,q,r) be the inertial velocity and inertial angular velocity vectors expressed in B. I get the scalar equations of motion as (assuming that the angular velocity is only along \hat{z}_b):
m \dot{u} - \frac{ml}{2} r^2 = F_{x_b}
m \dot{v} + \frac{ml}{2} \dot{r} = F_{y_b}
m \dot{w} = F_{z_b}
0 = M_{x_b}
-\frac{ml}{2} \dot{w} = M_{y_b}
\frac{ml^2}{3} \dot{r} + \frac{ml}{2} \dot{v} = M_{z_b}
The applied moment is given as : M_{z_b}(t) = 160 \left(1 - \cos \left(\frac{2 \pi t}{15} \right) \right). For t > 15, M_{z_b} = 0. See figure below :
Integrating these equations using MATLAB's ode45, I get the following plot :
From the above figure :
1) There is only one component of angular velocity (yaw rate) which is as expected. But is the magnitude correct (ie should it reach 24 rad/s)?
2) I am not able to figure out what's going on with u. Why is it increasing so rapidly?
Any help would be really appreciated.
yogesh
Last edited: