Question about the x term in time dilation

[Platformance]

When I first learned time dilation I was given this equation proven using the light clock example.

t = γt'

However, when I looked into the topic in more detail, I was given this equation.

t = γ(t' + xv/c²)

If x represents the distance between 2 frames, then does x have to change consistently as 1 frame moves away from the other?

 

[ghwellsjr]

When I first learned time dilation I was given this equation proven using the light clock example.

t = γt'

However, when I looked into the topic in more detail, I was given this equation.

t = γ(t' + xv/c²)

If x represents the distance between 2 frames, then does x have to change consistently as 1 frame moves away from the other?

Where'd you get that second equation from? It looks like a messed up version of the equation for the time coordinate for the Lorentz Transformation which is used to convert the coordinates of an event in one Inertial Reference Frame (IRF) into the coordinates of a second IRF moving at speed v along the x-axes.

 

[Nugatory]

When I first learned time dilation I was given this equation proven using the light clock example.

t = γt'

However, when I looked into the topic in more detail, I was given this equation.

t = γ(t' + xv/c²)

The first equation describes time dilation, the way that one observer's time interval may not be the same as another's. You could save yourself some confusion by writing it as $\Delta{t}=\gamma\Delta{t'}$ instead, to emphasize that it is about the interval between t values, not the t values themselves.

The second equation is one of the Lorentz transformations (written a bit oddly). These tell us how to convert one observer's statement "At time t and position x something happened" into t' and x' values that would make sense to the other observer looking at the same event.

The Lorentz transformations are far more basic and important than the time dilation formula. In fact, you can easily derive the time dilation formula from the Lorentz transformations by working with statements of the form "At time $t$, a clock was at position $x$ and its hands were pointing to ...".

If x represents the distance between 2 frames, then does x have to change consistently as 1 frame moves away from the other?

Yes. I'm driving a car, I'll say that the tip of my nose is the point x=0. If you're sitting by the side of the road watching me drive past, you would say that the position of the tip of my nose is x'=vt' where x' and t' are your time and distance measurements and v is our relative speed; intuitively, the longer you watch me drive away, the farther away from you the tip of my nose is.

 

[Platformance]

So x is the distance between frames, then this is my problem.

Suppose a spaceship travels past at 0.5c, the spaceship passes an observer on a planet.
The observer measures 1 second on his clock and a clock on the spaceship will spin for 0.75s using the time dilation formula.

However, after 1 second, the spaceship is 0.5c meters away from the planet. If the observer on the planet measures another second, does the clock on the spaceship pass 0.75s or 0.25s? 0.25s by using t = γ(t' + xv/c2) and making x = 0.5c.

 

[ghwellsjr]

So x is the distance between frames, then this is my problem.

Suppose a spaceship travels past at 0.5c, the spaceship passes an observer on a planet.
The observer measures 1 second on his clock and a clock on the spaceship will spin for 0.75s using the time dilation formula.

However, after 1 second, the spaceship is 0.5c meters away from the planet. If the observer on the planet measures another second, does the clock on the spaceship pass 0.75s or 0.25s? 0.25s by using t = γ(t' + xv/c2) and making x = 0.5c.

I cannot figure out what you are doing. Could you show your intermediate steps, including what your value for γ is and how you calculated it?

In the mean time, this is how I would do the calculation based on the correct Lorentz Transformation equation for time:

t' = γ(t - xv/c²)
where γ = 1/√(1-v²/c²)

At v = 0.5c, γ = 1/√(1-(0.5c)²/c²) = 1/√(1-0.25) = 1/√(0.75) = 1/0.866 = 1.1547

t' = γ(t - xv/c²) = 1.1547(1 - (0.5c)(0.5c)/c²) = 1.1547(1 - 0.25) = 1.1547(0.75) = 0.866

This, of course, does not match your value of 0.75 from the time dilation formula. But maybe if you would show how you calculated γ and how you applied the formula, we might be able to figure out why you got a different answer than I got.

Also, I'd like to repeat my question: where'd you get that second equation?

 

[ProfDawgstein]

When I first learned time dilation I was given this equation proven using the light clock example.

t = γt'

However, when I looked into the topic in more detail, I was given this equation.

t = γ(t' + xv/c²)

If x represents the distance between 2 frames, then does x have to change consistently as 1 frame moves away from the other?

t = γt'

is just the usual time dilation (how fast does the clock run in another system).

t = γ(t' + xv/c²)

is the lorentz transformation for the time variable.

The second part of the second equation ($xv/c^2$) has to do with simultaneity,
which basically says that if something happens to be in order AB for observer1 it does not have to
be AB for observer2. It could also be BA (if they are causually not related).

So x is the distance between frames, then this is my problem.

$x$ is the coordinate of an event in the $S$ reference frame.

Suppose a spaceship travels past at 0.5c, the spaceship passes an observer on a planet.
The observer measures 1 second on his clock and a clock on the spaceship will spin for 0.75s using the time dilation formula.

This should be correct if you used the correct values.

However, after 1 second, the spaceship is 0.5c meters away from the planet. If the observer on the planet measures another second, does the clock on the spaceship pass 0.75s or 0.25s? 0.25s by using t = γ(t' + xv/c2) and making x = 0.5c.

It should still be 0.75s.
This has nothing to do with $t = γ(t' + xv/c^2)$.
This equation describes events, not time itself.

Maybe you should check
-simultaneity (http://en.wikipedia.org/wiki/Relativity_of_simultaneity)
-synchronizing clocks
-time dilation
-lorentz transformations

It should be clear then.

 

[ghwellsjr]

I'm going to show you how you can use the Lorentz Transformation to analyze your scenario from post #4:

Suppose a spaceship travels past at 0.5c, the spaceship passes an observer on a planet.

Let's start in the rest IRF for the spacecraft :

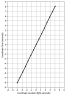
The black dots represent one-second intervals of time aligned with the Coordinate Times starting at -7 seconds to +7 seconds. Each dot represents an event with both a time and a location coordinate (along the x axis).

Now we want to transform these events into the rest IRF for the observer on the planet. To do this, we will note that as far as the spacecraft is concerned, the planet is traveling to the left at 0.5c so we want to use v=-0.5c. I like to use units where c=1, in this case seconds and light-seconds. This allows us to use simplified equations based on β=v/c and β=-0.5. The equation for gamma is:

γ = 1/√(1-β²)

I already evaluated this in post #5 so I won't do it again:

γ = 1.1547

Now we have to use both Lorentz Transformation equations:

t' = γ(t-xβ)
x' = γ(x-tβ)

Note that on the right side of the equations there are no primed terms, they are both on the left sides. The way you use these equations is you pick an event in the original IRF and plug its x (location) and t (time) coordinates into the equations to calculate the x' and t' coordinates for the same event in a second IRF moving at β with respect to the original IRF.

So let's use the uppermost event with coordinates of x=0 and t=7. Plugging these values into the two equations we get:

t' = γ(t-xβ) = 1.1547(7-0) = 8.0829
x' = γ(x-tβ) = 1.1547(0-7*(-0.5)) = 1.1547(3.5) = 4.04145

If we calculate the events for the bottom event we will see that it has the same values but they are the negatives.

Now you could repeat the calculations for all the other events or you could just realize that the dots will be equally spaced in the new IRF and just mark them in if you are drawing a diagram by hand. I use a computer program so we will get:

As you can see, the dots representing 1-second intervals are spaced farther apart--they are dilated. We call the time for the spacecaft, the Proper Time of the spacecraft . For convenience, we will call the Proper Time when the Coordinate Time is zero to also be zero and count the dots upwards or downwards from that point accordingly to determine the Proper Time of any other dot.

Now since this is the rest IRF of the observer on the planet, we can just draw him in using blue for his color:

Now I think you can see that at the observer's Coordinate Time of 1 second, the Proper Time of the spacecraft is a little less than 1 second. This is where your calculation comes in.

The event (not shown by a dot) that you want to consider has coordinates of t=1 and x=0.5 and β is now 0.5 (because the spacecraft is moving to the right in the planet's rest IRF). You just plug those into the same two equations we used before and get coordinates of:

t' = 0.866
x' = 0

I previously did the calculation for t' in post #5 so I won't repeat it here and you can see that the x' value evaluates to zero (as it must since we are transforming to the rest IRF of the spacecraft ).

 

[Platformance]

I think I am starting to understand this now, the second equation doesn't describe an interval of time, but a moment in time.

This equation t' = γ(t-xβ) (should this be t' = γ(t-tβ) instead?) calculates the time an event happens in the frame of s' given the time and position of the event happening in s. In the equation that I posted I forgot the ', it should say t = γ(t' + x'v/c2), hopefully this clears up my mistake.

Now I think you can see that at the observer's Coordinate Time of 1 second, the Proper Time of the spacecraft is a little less than 1 second.

I am not seeing where this part appears in the diagram, would the proper time of the spacecraft be the 0.866s calculated? The distance between 2 events in the spaceship appear to be the value of the Lorentz transform 1.1547.

 

[ghwellsjr]

I think I am starting to understand this now, the second equation doesn't describe an interval of time, but a moment in time.

This equation t' = γ(t-xβ) (should this be t' = γ(t-tβ) instead?)...

No, it is correct as I gave it. It's important to realize that events in Special Relativity require coordinates in both space and time and changing either part in one IRF will change both of the parts in the transformed IRF. That's why we refer to "spacetime".

... calculates the time an event happens in the frame of s' given the time and position of the event happening in s. In the equation that I posted I forgot the ', it should say t = γ(t' + x'v/c2), hopefully this clears up my mistake.

That form of the Lorentz Transformation is used for converting the coordinates of an IRF back to its original IRF without changing the sign of the velocity. You should use the form as I presented it with the negative sign between the terms when going from s to s'. Then you can use the form with the plus sign to go back from s' to s (without having to change the sign of v or β).

However, if you just use the same form all the time and consider s to be the "from" frame and s' to be the "to" frame, then you can use the same equations for going both ways as long as you are careful to adhere to the correct sign of v or β. One reason I prefer to do it this way is if you ever want to transform between three frames, then you have to invent new forms of the equations--why bother? Just understand what you're doing and you'll never have a problem.

Now I think you can see that at the observer's Coordinate Time of 1 second, the Proper Time of the spacecraft is a little less than 1 second.

I am not seeing where this part appears in the diagram, would the proper time of the spacecraft be the 0.866s calculated?

Yes.

The distance between 2 events in the spaceship appear to be the value of the Lorentz transform 1.1547.

Yes, the Coordinate Distance in seconds of time between 2 events that are separated by 1 second of Proper Time is the Lorentz Factor, gamma, which is 1.1547. More precisely, the difference in Coordinate Time divided by the difference in Proper Time is gamma.

 

[Platformance]

The equation t = γ(t' + x'v/c²) creates t = γ(t' + t'β) with β=v/c and t' = x'/c, or t' = γ(t - xv/c²) into t' = γ(t - tβ).
I am not sure where t' = γ(t - xβ) comes from.

That form of the Lorentz Transformation is used for converting the coordinates of an IRF back to its original IRF without changing the sign of the velocity.

Are you talking about t = γ(t' + x'v/c²) or t' = γ(t - xβ)?

 

[ghwellsjr]

The equation t = γ(t' + x'v/c²) creates t = γ(t' + t'β) with β=v/c and t' = x'/c, or t' = γ(t - xv/c²) into t' = γ(t - tβ).
I am not sure where t' = γ(t - xβ) comes from.

If you start with the standard Lorentz Transformation equations as given by just about everyone, including wikipedia (just below the subheading, "Boost in the x-direction"), you have:

t' = γ(t - vx/c²)

But if we substitute β for v/c and use units where c=1 (seconds for time and light-seconds for location) then it becomes:

t' = γ(t - βx) or γ(t - xβ)

That form of the Lorentz Transformation is used for converting the coordinates of an IRF back to its original IRF without changing the sign of the velocity.

Are you talking about t = γ(t' + x'v/c²) or t' = γ(t - xβ)?

I'm talking about t = γ(t' + x'v/c²). This is also mentioned in the wikipedia article (just above the subheading, "Boost in the y or z directions"), where they talk about the inverse transformations.

I still haven't seen your original calculations. How did you get 0.25s in the last sentence of post #4?

 

[Platformance]

So t' = γ(t - vx/c²) and t' = γ(t - xβ) are the same except x in the second equation is in the unit of light seconds. I assume this also applies to x' = γ(x-tβ), where x' = γ(x-vt), v = β/c and c = 1.

As for the 0.75s and 0.25s, I realized I forgot the square root when I solved for γ, so those values are wrong.

Going back to the diagram with the spaceship example, the proper time in the spaceship is 0.866s, but I don't see 0.866 in the diagram. Is 0.866 the distance between 2 blue dots if the distance between 2 black dots is 1?

 

[ghwellsjr]

So t' = γ(t - vx/c²) and t' = γ(t - xβ) are the same except x in the second equation is in the unit of light seconds. I assume this also applies to x' = γ(x-tβ), where x' = γ(x-vt), v = β/c and c = 1..

Yes, except we could use a bunch of other pairs of units such as years and light-years or even one of my favorites, nanoseconds and feet.

As for the 0.75s and 0.25s, I realized I forgot the square root when I solved for γ, so those values are wrong.

But even if you hadn't forgotten the square root, I still don't understand how you got the second number significantly less than the first number. Can you please show me your calculation?

Going back to the diagram with the spaceship example, the proper time in the spaceship is 0.866s, but I don't see 0.866 in the diagram. Is 0.866 the distance between 2 blue dots if the distance between 2 black dots is 1?

I think you may have the right idea, but you really should think in terms of the Coordinate Time, not the blue Proper Time for several reasons:

Firstly, the blue Proper Time applies just to the blue observer on the planet which remains localized at x=0 in this IRF, whereas the spaceship is only at x=0 for an instant in time (t=0). On the other hand, the Coordinate Time applies everywhere.

Secondly, the blue observer doesn't have to remain stationary, he could take off in his own spaceship at some high speed, in which case his own Proper Time world be dilated and no longer related to the Proper Time of the black spaceship.

Thirdly, we don't even need the blue observer as is the case in the second diagram in post #7.

Fourthly, we can transform to a different IRF in which both the blue observer and the black spaceship are traveling at new speeds with new gamma values and new time dilations with new spacings of the Proper Time dots which will always have the correct ratios with respect to the Coordinate Time.

So the Proper Time interval from t=0s to t=0.866s, is 86.6% of the vertical distance from the position on the graph of the black dot (which is obscured by the blue dot at the same position) to the next black dot upwards and occurs exactly at the Coordinate Time of 1s.

I have drawn a zoomed in diagram and added a red dot at the coordinates of t=1 and x=0.5:

Now I let my program redraw the diagram with β=0.5. This transforms the rest IRF of the blue observer on the planet to the rest IRF of the black spaceship:

Now the red dot has the coordinates that were calculated previously and I think you can see that it is 86.6% of the way from the Proper Time of 0s to the Proper Time of 1s for the black spaceship.

And, as I said earlier, we can also transform to any other IRF such as this one where both the blue observer on the planet and the black spaceship are traveling apart from each other at 0.268c:

Now you can see that both the observer and the spaceship are time dilated by the same amount (1.038) and yet the red dot is still 86.6% of the way from the dot at t=0 to the next black dot up. However, the red dot has no significance in this diagram--it doesn't represent anything except to show that it is at the same Proper Time for the spaceship. Note that the red dot is just below the Coordinate Time of 1 second while the black dot above it is above the Coordinate Time of 1 second. The whole point of this exercise is to make clear that Time Dilation is different in different IRF's and is unobservable by the observers on the planet or spaceship. No observer has any awareness of their own Time Dilation or the Time Dilation of any other observer. How could they? It changes when we choose a different IRF to represent the scenario.

 

[ghwellsjr]

As I mentioned at the end of the previous post, no observer can see or have any awareness of the Time Dilation of anyone else and now I want to show you what they can observe. We do this by drawing in light signals along 45-degree paths from an event at one observer to the other observer and we will see that it doesn't matter what IRF we use, the Proper Time at which an observer gets the light signals from another observer remains the same.

We start with the rest IRF of the blue observer on the planet as he is watching the spaceship approach, pass, and depart from him:

The first signal I have drawn in starts at the black spaceship's Proper Time of -7s (you have to count the dots down from the dot representing 0s where the spaceship and the planet coincide) and it goes up and to the right to the blue observer's Proper Time of -4s. So the blue observer actually sees the clock on the spaceship displaying -7s when his own clock displays -4s.

Then when the spaceship passes him, he sees both their clocks displaying 0s. So he would say that he is seeing the spaceships clock ticking 7/4 or 1.75 times the rate of his own. This is called Relativistic Doppler and there is a formula to calculate it which you can look up in wikipedia if you want. That formula gives a more exact value of 1.732051 but this is close enough for simply eye-balling values off a diagram.

The second signal I drew in starts at the black spaceship's Proper Time of +4s and goes up and to the left to the blue observer's Proper Time of +7s. Now he would say that it appears that the spaceship's clock is ticking at 4/7 or 0.571 times the rate of his own. The formula gives about 0.57735.

So neither one of these ratios is the correct Time Dilation of 1.1547 for this IRF. However, if we average the two Relativistic Doppler factors that we measured or calculated, we would get the correct Time Dilation factor:

(7/4 + 4/7)/2 = (49/28 + 16/28)/2 = (65/28)/2 = 2.3214/2 = 1.1607

Or more precisely using the Relativistic Doppler formula values:

(1.732051+0.57735)/2 = 2.309401/2 = 1.1547

Now let's look at the rest IRF for the spaceship:

As you can see, the blue observer still sees the same comparative rates of the spaceship's clock and he makes all the same calculations but in this IRF, it is his own clock that is Time Dilated, not the spaceship's and so he gets the "wrong" answer. Or we could reinterpret what he is calculating and say that he is determining what the spaceship's Time Dilation would be in his own rest IRF even if we are analyzing the scenario from a different IRF.

Finally, let's look at the IRF in which both the observer and the spaceship are traveling at the same speed in opposite directions (0.268c):

Once again, all observations and calculations remain the same even though in this IRF the Time Dilations of the observer and the spaceship are identical.

 

[Imager]

@ghwellsjr,

Thank you for the great explanation! I've been trying to get this to work right in an Excel spreadsheet for years and thanks to you it finally works!

 

[Platformance]

So the 0.866s represents a fraction of distance between the points for the black line and not the total distance, but the black dots are a distance 1.1547 away. Does this mean that when the planet's clock tick 1 second, the observer sees an event, but when the clock ticks 1.1547 seconds, the spaceship sees an event?

As for the 0.25s, I don't quite remember what my calculations were. However, I did the calculation by thinking that t = γ(t' + x'v/c2) was an expanded version of the time dilation formula since I wasn't quite sure what the equation meant. I thought the period of time dilation changed as one frame moved away from another frame.

 

[ghwellsjr]

So the 0.866s represents a fraction of distance between the points for the black line and not the total distance, but the black dots are a distance 1.1547 away.

Take a look at this diagram which is basically the same as the first one in post #13, except I have added labels to show the Proper Times displayed on the blue clock traveling with the observer on the planet and the Proper Times displayed on the black clock traveling with the spaceship:

So 0.866s (where the red dot is) represents the Proper Time on the black clock when it gets to the Coordinate Time of 1 second. The black dot at the Proper Time of 1 second is at the Coordinate Time of 1.1547s.

Does this mean that when the planet's clock tick 1 second, the observer sees an event...

When the planet's clock ticks 1 second, the observer sees the event of his own clock displaying 1 second, and he also sees the spaceship's clock at 0.577s which is approximately 4/7, the same ratio discussed in post #14 after the first diagram.

...but when the clock ticks 1.1547 seconds, the spaceship sees an event?

When the observer's clock ticks 1.1547 seconds, the Coordinate Time is also 1.1547 seconds which is when the spaceship sees the event of its own clock displaying the Proper Time of 1 second. (But this is true only in this IRF, in other IRF's it may not be true.)

As for the 0.25s, I don't quite remember what my calculations were. However, I did the calculation by thinking that t = γ(t' + x'v/c2) was an expanded version of the time dilation formula since I wasn't quite sure what the equation meant. I thought the period of time dilation changed as one frame moved away from another frame.

Time Dilation is not an effect that involves multiple frames. It is an effect that applies to every clock in a single frame and is a function of the speeds of the clocks in that frame. When you transform all the events from one frame to another frame moving with respect to the first frame, then all the clocks may have different speeds and therefore different Time Dilations.

 

[Platformance]

Thank you for all your help! =)

So to summarize:

When the observer's clock ticks 1 second, the spaceship's clock ticks 0.866s from time dilation.

At 1 second, the observer sees an event and sees the spaceship's clock at 0.577s due the relativistic doppler effect (I couldn't find the equation for this when I searched it up, I only found equations dealing with frequency).

When the observer's clock ticks 1.1547s, the spaceship's clock ticks 1 second and the spaceship sees an event.

t' = γ(t-xβ) and x' = γ(x-tβ) are not time dilation and length contraction equations, they transform the time and position of an event from 1 frame to another.

 

[ProfDawgstein]

When the observer's clock ticks 1 second, the spaceship's clock ticks 0.866s from time dilation.

Yes, if you are in the frame of the observer.

At 1 second, the observer sees an event and sees the spaceship's clock at 0.577s due the relativistic doppler effect (I couldn't find the equation for this when I searched it up, I only found equations dealing with frequency).

This has nothing to do with the doppler effect.
The doppler effect describes the change of frequency (frequency shift of light).
Just transform between the reference frames using the lorentz transformations and everything should be fine.

t' = γ(t-xβ) and x' = γ(x-tβ) are not time dilation and length contraction equations, they transform the time and position of an event from 1 frame to another.

Yes

 

[ghwellsjr]

Thank you for all your help! =)

So to summarize:

When the observer's clock ticks 1 second, the spaceship's clock ticks 0.866s from time dilation.

Whenever you make a statement like this, you need to state which frame it applies to as ProfDawgstein pointed out. In the rest IRF of the observer it is true but in the rest IRF of the spaceship, the opposite is true. And in other IRF's, such as the last one in post #13, both clocks tick at the same rate. Time dilation is frame dependent and you should really think of it as a coordinate effect as I tried to point out in post #13. In other words, in our example, it's the ratio of the coordinate time to the time on a clock, not fundamentally the times between two clocks. That's why it's so important to state which frame it applies to.

At 1 second, the observer sees an event and sees the spaceship's clock at 0.577s due the relativistic doppler effect (I couldn't find the equation for this when I searched it up, I only found equations dealing with frequency).

But we are dealing with frequency, namely the frequency of the one-second ticks of the clocks, which tick at a frequency of 1 Hz. Knowing that, can you go back and see how the equation determines the rate that each observer sees the other ones clock ticking at compared to their own, both while the spaceship is approaching the observer and while the spaceship is receding from the observer?

Note that the relativistic Doppler effect is not frame dependent--it doesn't matter what frame you are using to describe or analyze the effect.

When the observer's clock ticks 1.1547s, the spaceship's clock ticks 1 second...

Again, this is true only in the rest IRF of the observer.

...and the spaceship sees an event.

Yes, but you didn't say what time on the observer's clock the spaceship sees when its clock ticks 1 second. Do you want to try to answer that question? (HINT: it's real easy.)

t' = γ(t-xβ) and x' = γ(x-tβ) are not time dilation and length contraction equations, they transform the time and position of an event from 1 frame to another.

Yes, again as ProfDawgstein pointed out.

 

[Platformance]

Time dilation is frame dependent and you should really think of it as a coordinate effect as I tried to point out in post #13.

Could you please explain what you mean by a coordinate effect, the way I see it the coordinate time is the proper time in the reference frame that the calculations are based on.

But we are dealing with frequency, namely the frequency of the one-second ticks of the clocks, which tick at a frequency of 1 Hz. Knowing that, can you go back and see how the equation determines the rate that each observer sees the other ones clock ticking at compared to their own, both while the spaceship is approaching the observer and while the spaceship is receding from the observer?

The equation I found was:

\nu_{observed} = \nu_{source} \sqrt{\frac{1+\beta}{1-\beta}}

\nu_{observed} comes out to be 0.577 when \nu_{source} is 1 and when β is -0.5.

Is β -0.5 because the light is traveling in the opposite direction?

Yes, but you didn't say what time on the observer's clock the spaceship sees when its clock ticks 1 second. Do you want to try to answer that question? (HINT: it's real easy.)

Is the answer 0.577s?

 

[ghwellsjr]

Time dilation is frame dependent and you should really think of it as a coordinate effect as I tried to point out in post #13.

Could you please explain what you mean by a coordinate effect, the way I see it the coordinate time is the proper time in the reference frame that the calculations are based on.

Let's review:

Here is the first diagram I made for you from post #7 showing the rest IRF for the spaceship:

Note that the speed of the spaceship in this IRF is zero and therefore gamma is 1 and the Time Dilation factor is 1, which means that the spaceship's clock ticks at the same rate as the coordinate time. Even though the Proper Time on the spaceship's clock is the same as the Coordinate Time, we realize that they are not the same thing because the spaceship's Proper Time only applies at the location of the spaceship (where the thick black line is), while the Coordinate Time applies everywhere. We could pick any random point on the graph and we could specify an event with its Coordinate Location and Coordinate Time by looking at the corresponding grid lines (and interpolating if necessary).

Now the second diagram I made for you shows what you get when you transform the coordinates of all the events of the first graph to a speed of -0.5c:

You will note that the spaceship has a new speed, 0.5c, a new gamma, 1.1547, and a new Time Dilation factor of 1.1547. Therefore, speed, gamma, and Time Dilation factor are all coordinate effects--they depend on the coordinates of the IRF in which we are describing the scenario. You will notice that there is no clock in this IRF whose Proper Time matches the Coordinate Time but we do see that the ratio of the Coordinate Time to the Proper Time of the spaceship's clock has the correct Time Dilation factor.

But we are dealing with frequency, namely the frequency of the one-second ticks of the clocks, which tick at a frequency of 1 Hz. Knowing that, can you go back and see how the equation determines the rate that each observer sees the other ones clock ticking at compared to their own, both while the spaceship is approaching the observer and while the spaceship is receding from the observer?

The equation I found was:

\nu_{observed} = \nu_{source} \sqrt{\frac{1+\beta}{1-\beta}}

\nu_{observed} comes out to be 0.577 when \nu_{source} is 1 and when β is -0.5.

That is correct for the case that I drew where the spaceship is receding away from the observer but what about when the spaceship is approaching the observer?

Is β -0.5 because the light is traveling in the opposite direction?

The sign of the speed has to be defined and can be different in other derivations. For example, if you look at Einstein's 1905 paper introducing Special Relativity (2/3 of the way down in section 7), you will see the opposite convention. It really is simple; if the two observers are receding, the Relativistic Doppler factor is less than 1 and if they are approaching, it is greater than one. Note also that they are inverses of each other.

Yes, but you didn't say what time on the observer's clock the spaceship sees when its clock ticks 1 second. Do you want to try to answer that question? (HINT: it's real easy.)

Is the answer 0.577s?

Yes.

 

[Platformance]

Let's review:

Even though the Proper Time on the spaceship's clock is the same as the Coordinate Time, we realize that they are not the same thing because the spaceship's Proper Time only applies at the location of the spaceship (where the thick black line is), while the Coordinate Time applies everywhere. We could pick any random point on the graph and we could specify an event with its Coordinate Location and Coordinate Time by looking at the corresponding grid lines (and interpolating if necessary).

So in the rest frame of the spaceship, the coordinate time and proper time are only equal at x = = 0. If an event happens anywhere else, the time that the event happens is the coordinate time, but there is no proper time because the spaceship does not pass through the event.

That is correct for the case that I drew where the spaceship is receding away from the observer but what about when the spaceship is approaching the observer?

\nu_{observed} = \nu_{source} \sqrt{\frac{1+\beta}{1-\beta}}

\sqrt{\frac{1+\beta}{1-\beta}} is 1.732.

Using the diagram from post 16, if the light is sent from the spaceship's time of -1s to the observer, then:

\nu_{observed} = -1
\nu_{source} = -0.577

The blue observer sees the spaceship's clock at -1 when its own clock is at -0.577.

One more thing though, going back to the diagram in post 16, an event happens on the spaceship at its proper time of -1s, from the doppler effect formula, the blue observer sees that event at t = -0.577. However, the blue observer already has an event at its proper time of -1s, are the black dots and blue dots the same events transformed or different events?

 

[ghwellsjr]

So in the rest frame of the spaceship, the coordinate time and proper time are only equal at x = = 0. If an event happens anywhere else, the time that the event happens is the coordinate time, but there is no proper time because the spaceship does not pass through the event.

Yes.

\nu_{observed} = \nu_{source} \sqrt{\frac{1+\beta}{1-\beta}}

\sqrt{\frac{1+\beta}{1-\beta}} is 1.732.

Correct.

Using the diagram from post 16, if the light is sent from the spaceship's time of -1s to the observer, then:

\nu_{observed} = -1
\nu_{source} = -0.577

(I think you mean the diagram from post 17.)

You got the source and observed interchanged. If you put them in the right order, you will get the same answer you got using the equation.

The blue observer sees the spaceship's clock at -1 when its own clock is at -0.577.

This is correct but you need to do the division to get the same answer as the equation.

One more thing though, going back to the diagram in post 16, an event happens on the spaceship at its proper time of -1s, from the doppler effect formula, the blue observer sees that event at t = -0.577. However, the blue observer already has an event at its proper time of -1s, are the black dots and blue dots the same events transformed or different events?

Each dot is a separate event. It might help if you go back and read all my posts.

 

[Platformance]

You got the source and observed interchanged. If you put them in the right order, you will get the same answer you got using the equation.

Isn't \nu_{source} the observer time and \nu_{observed} the spaceship time? When the spaceship time is -1 the observer time is -0.577.

Each dot is a separate event. It might help if you go back and read all my posts.

I think I understand now:

The equations t' = γ(t-xβ) and x' = γ(x-tβ) replicate an event from 1 frame to another.

When the clock on the planet strikes 1 at t = 1 and x = 0, t' = 1.1547 and x' = 0.577 are the coordinates when the spaceship's clock strikes 1. t' and x' are not the coordinates when the spaceship sees the observer's clock strike 1, those coordinates are found using the relativistic doppler.

 

[ghwellsjr]

Isn't \nu_{source} the observer time and \nu_{observed} the spaceship time? When the spaceship time is -1 the observer time is -0.577.

That's also true but I was trying to get you to do it for the observer while the spaceship was approaching since you had already done it while the spaceship was receding.

I think I understand now:

The equations t' = γ(t-xβ) and x' = γ(x-tβ) replicate an event from 1 frame to another.

Yes, but realize that each frame is represented in a separate diagram that shows both the observer and the spaceship.

When the clock on the planet strikes 1 at t = 1 and x = 0, t' = 1.1547 and x' = 0.577 are the coordinates when the spaceship's clock strikes 1. t' and x' are not the coordinates when the spaceship sees the observer's clock strike 1, those coordinates are found using the relativistic doppler.

No. As I said before, you need to be clear about what frame you are talking about whenever you make statements about "when this, then that. Simultaneity always means that the time coordinates for two events have the same value. So in the IRF on post #17, when the clock on the planet strikes 1 at t = 1 and x = 0, the coordinates of the spaceship are t = 1 and x = 0.5 (remember it is traveling at 0.5c in this frame). At that event, the Proper Time on the spaceship is 0.866 as indicated on the diagram.

If you want to determine when the spaceship sees the planet's clock strike 1, you need to draw a diagonal line from the point where that event happens upward and to the right at a 45 degree angle and it will encounter the spaceship at t = 2 and x = 1. The spaceship's Proper Time will be 1.732.

 

[Platformance]

No. As I said before, you need to be clear about what frame you are talking about whenever you make statements about "when this, then that. Simultaneity always means that the time coordinates for two events have the same value. So in the IRF on post #17, when the clock on the planet strikes 1 at t = 1 and x = 0, the coordinates of the spaceship are t = 1 and x = 0.5 (remember it is traveling at 0.5c in this frame). At that event, the Proper Time on the spaceship is 0.866 as indicated on the diagram.

If you want to determine when the spaceship sees the planet's clock strike 1, you need to draw a diagonal line from the point where that event happens upward and to the right at a 45 degree angle and it will encounter the spaceship at t = 2 and x = 1. The spaceship's Proper Time will be 1.732.

Okay the frame I was dealing with would be the frame of the planet in the diagram on post 17. At t = 1 and x = 0 in the frame of the planet, t' =1.1547. 1.1547 is the coordinate time, but the proper time on the spaceship is 1. The observer does not see the spaceship clock at 1 when the coordinate time is 1.1547, but instead at coordinate time 1.732 (calculated using the relativistic doppler). Finally, the proper time of the spaceship when the coordinate time is 1.732 is 1.12 (calculated using time dilation).

 

[ghwellsjr]

Okay the frame I was dealing with would be the frame of the planet in the diagram on post 17.

To be clear, you should say "the rest frame of the planet" because when you say "the frame of the planet", it seems like you are excluding the spaceship. I just want to make sure you understand that it's the frame in which the planet is at rest and in which the spaceship is moving.

At t = 1 and x = 0 in the frame of the planet, t' =1.1547.

Why did you use the Lorentz Transformation equation for time here? You said in post #19 that "The equations t' = γ(t-xβ) and x' = γ(x-tβ) replicate an event from 1 frame to another". Since you are only considering one frame, the rest frame of the planet (which is also the moving frame of the spaceship), why are you concerned about a Coordinate Time in a different frame?

1.1547 is the coordinate time, but the proper time on the spaceship is 1.

I get the impression that you determined this coordinate time by transforming the event of the planet's Proper Time = 1. If so, it has nothing to do with the event of spaceship's Proper Time = 1. If you want to know the Coordinate Time of the event of the spaceship's Proper Time = 1, you do it like this:

The spaceship is traveling at 0.5c. Gamma at this speed if 1.1547. Since the ratio of the Coordinate Time to the Proper Time for the spaceship in this scenario is equal to gamma and since the Proper Time is 1, then the Coordinate Time is equal to the product of the Proper Time and gamma which is 1.1547.

The observer does not see the spaceship clock at 1 when the coordinate time is 1.1547, but instead at coordinate time 1.732 (calculated using the relativistic doppler).

Correct. You can verify this by drawing a diagonal line at 45-degrees going from the event of the spaceship's clock at 1 upward and to left until it intersects with the planet's clock.

Finally, the proper time of the spaceship when the coordinate time is 1.732 is 1.12 (calculated using time dilation).

This is not correct. You can get from Coordinate Time to Proper Time in this scenario by dividing by gamma so it would be 1.732/1.1547 = 1.5. How did you get 1.12?

I have added lines into the drawing from post #17 to show the issues on this post:

 

[Platformance]

Why did you use the Lorentz Transformation equation for time here? You said in post #19 that "The equations t' = γ(t-xβ) and x' = γ(x-tβ) replicate an event from 1 frame to another". Since you are only considering one frame, the rest frame of the planet (which is also the moving frame of the spaceship), why are you concerned about a Coordinate Time in a different frame?

I was trying to say that an event happens at coordinate time 1.1547 in the rest inertial frame of the planet, but this event happens at the spaceship's proper time of 1.

I get the impression that you determined this coordinate time by transforming the event of the planet's Proper Time = 1. If so, it has nothing to do with the event of spaceship's Proper Time = 1. If you want to know the Coordinate Time of the event of the spaceship's Proper Time = 1, you do it like this:

The spaceship is traveling at 0.5c. Gamma at this speed if 1.1547. Since the ratio of the Coordinate Time to the Proper Time for the spaceship in this scenario is equal to gamma and since the Proper Time is 1, then the Coordinate Time is equal to the product of the Proper Time and gamma which is 1.1547.

So the time dilation equation, t' = γt. Where in the rest inertial frame of the planet, t' is the coordinate time, t is the spaceship's proper time.

This is not correct. You can get from Coordinate Time to Proper Time in this scenario by dividing by gamma so it would be 1.732/1.1547 = 1.5. How did you get 1.12?

My mistake, I think I divided 1.732/1.547 instead of 1.732/1.1547 by accident.

 

[ghwellsjr]

I was trying to say that an event happens at coordinate time 1.1547 in the rest inertial frame of the planet, but this event happens at the spaceship's proper time of 1.

Good, that is correct.

So the time dilation equation, t' = γt. Where in the rest inertial frame of the planet, t' is the coordinate time, t is the spaceship's proper time.

Do you realize that this equation is the opposite of the similar one that you presented in your first post? It's always confusing when two forms of t are used, one primed and the other unprimed. There is a better, clear and common way to present the equation and that is using the Greek letter tau, τ, to represent the Proper Time leaving t (and t') to always represent Coordinate Time. You can state it as t = γτ or its incremental version, Δt = γΔτ, which is usually more useful because if you are drawing a diagram for an observer/object/clock traveling at some speed, you can easily calculate γ and then you can calculate how far in Coordinate Time to place a dot representing some increment of Proper Time. This is what my computer program does when I specify an original IRF.

My mistake, I think I divided 1.732/1.547 instead of 1.732/1.1547 by accident.

Good, I'm glad it was just a caculation mistake. (That's one advantage of using a computer program.) It appears that you are getting a pretty good grasp on these ideas. Since you're such a good learner, I'd like to continue on with some more ideas as time permits.

 

[Platformance]

Do you realize that this equation is the opposite of the similar one that you presented in your first post? It's always confusing when two forms of t are used, one primed and the other unprimed. There is a better, clear and common way to present the equation and that is using the Greek letter tau, τ, to represent the Proper Time leaving t (and t') to always represent Coordinate Time. You can state it as t = γτ or its incremental version, Δt = γΔτ, which is usually more useful because if you are drawing a diagram for an observer/object/clock traveling at some speed, you can easily calculate γ and then you can calculate how far in Coordinate Time to place a dot representing some increment of Proper Time. This is what my computer program does when I specify an original IRF.

I see, I wasn't quite sure of how the time dilation equation worked when I started this thread, but I understand it more clearly now.

Good, I'm glad it was just a caculation mistake. (That's one advantage of using a computer program.) It appears that you are getting a pretty good grasp on these ideas. Since you're such a good learner, I'd like to continue on with some more ideas as time permits.

Thank you! The graphs and explanation made this concept much easier to understand, and I didn't expect to learn the relativistic doppler when I started this thread. I am still learning relativity (currently on the spacetime interval) and I am sure more ideas will appear.

 

[yuiop]

So the 0.866s represents a fraction of distance between the points for the black line and not the total distance, but the black dots are a distance 1.1547 away. Does this mean that when the planet's clock tick 1 second, the observer sees an event, but when the clock ticks 1.1547 seconds, the spaceship sees an event?

They are two different clocks. It means that both the planet observer and the spaceship observer see 1 second indicated on the planet clock and 0.866s on the spaceship clock at the same event if they are both momentarily alongside the event and each other, but their clocks read differently because they are ticking at different rates in any given reference frame. At the later event, if both observers are at the same event alongside each other, then both observers see 1.1547 seconds on the planet clock and 1 second on the spaceship clock. Note, that in order to do this we need an array of observers with synchronised clocks on the planet, so that we can conveniently have observers local to the events when they occur.

By, the way, you are getting your units mixed up. 0.866s is in units of time and you are using it to mean distance. Earlier you said x = 0.5c which is a velocity, but x is a distance. You need to be careful about units to avoid confusion.

I thought the period of time dilation changed as one frame moved away from another frame.

This is not correct. When two clocks are moving with constant sped relative to each other, their distance apart is continually changing, but the time dilation remains constant. Earlier ghwellsjr gave a worked example for a clock that started at t=0 and x=0, and ended at t=1 and x=0.5 and calculated that the time on the spaceship clock would be t' = 0.866s when t=1:

... In the mean time, this is how I would do the calculation based on the correct Lorentz Transformation equation for time:

t' = γ(t - xv/c²)
where γ = 1/√(1-v²/c²)

At v = 0.5c, γ = 1/√(1-(0.5c)²/c²) = 1/√(1-0.25) = 1/√(0.75) = 1/0.866 = 1.1547

t' = γ(t - xv/c²) = 1.1547(1 - (0.5c)(0.5c)/c²) = 1.1547(1 - 0.25) = 1.1547(0.75) = 0.866

...

Now let's see what happens if a clock in the spaceship was initially at x=1 at time t=0. This spaceship clock would initially be reading: t'₀ = γ(0s-(1ls * 0.5c)/c^2 ) = -0.57735s

This is using the convention that the origins of the frames coincided at x=0, t=0, x'=0 and t'=0.

Now after 1 second as measured in the planet ref frame (S) the spaceship clock will be at x=1.5 light seconds, so we can calculate the time indicated in the spaceship ref frame (S') as t'₁ = 1.1547(1s-(1.5ls * 0.5c)/c^2 ) = 0.28867s for this event.

The elapsed time between these two events is 1 second in frame S and Δt' = t'₁ - t'₀ = 0.28867 - (-0.57735) = 0.866 seconds in frame S'.

You can now see that the time dilation factor is still the same (0.866 seconds in S' for every second in S or a time dilation factor of 1/0.866 = 1.1547) despite the clock being further away.

Note that two calculations done above to calculate the coordinates of the events and then subtracting them to get the difference interval can be done a single calculation as:

Δt' = γ(Δt - Δx * v/c²) = 1.1547( 1 - 0.5*0.5) = 0.866s.

While the Lorentz transformation can be used to calculate transformed intervals and instantaneous coordinates, the time dilation formula can only be used with intervals. In other words the time dilation formula can tell you that one clock is running slower than another by a factor of 1.1547 but it cannot tell you that when a clock in S is reading 3PM that a clock in S' is reading 2PM, whereas the Lorentz transformation can.

 

[ghwellsjr]

They are two different clocks. It means that both the planet observer and the spaceship observer see 1 second indicated on the planet clock and 0.866s on the spaceship clock at the same event if they are both momentarily alongside the event and each other, but their clocks read differently because they are ticking at different rates in any given reference frame.

I understand what you are trying to communicate in the above sentence but since you redefined standard relativity terms without stating what you are doing, then it can only lead to confusion for someone who is trying to learn relativity.

First, you are using the word "see" differently than I have been using it in this thread. "See" means what you observe with your eyes and that's not what you mean here. Could you please define what you mean by "see"?

Second, you are using the word "event" differently than I have ever heard anyone use it in a discussion about relativity. Could you please define what you mean by "event"?

At the later event, if both observers are at the same event alongside each other, then both observers see 1.1547 seconds on the planet clock and 1 second on the spaceship clock. Note, that in order to do this we need an array of observers with synchronised clocks on the planet, so that we can conveniently have observers local to the events when they occur.

I don't see why we need this array of observers. Maybe you should explain exactly where they are located and exactly what they see and exactly when they see it.

By, the way, you are getting your units mixed up. 0.866s is in units of time and you are using it to mean distance. Earlier you said x = 0.5c which is a velocity, but x is a distance. You need to be careful about units to avoid confusion.

No, he's not getting the units mixed up. If you read carefully, you will see that he was referring to the distance on the diagram between two dots on the thick black line so that he could apply the correct ratio to establish where 0.866 seconds would be.

...

Now let's see what happens if a clock in the spaceship was initially at x=1 at time t=0. This spaceship clock would initially be reading: t'₀ = γ(0s-(1ls * 0.5c)/c^2 ) = -0.57735s

This is using the convention that the origins of the frames coincided at x=0, t=0, x'=0 and t'=0.

Usually, when we set the origins of two frames to coincide, we also synchronize the two clocks to zero at that event. I don't see where you synchronized the two clocks in your new example. Until you do that, I don't see how you can just say the spaceship clock had some reading on it at some location distant from the planet clock.

Now after 1 second as measured in the planet ref frame (S) the spaceship clock will be at x=1.5 light seconds, so we can calculate the time indicated in the spaceship ref frame (S') as t'₁ = 1.1547(1s-(1.5ls * 0.5c)/c^2 ) = 0.28867s for this event.

The elapsed time between these two events is 1 second in frame S and Δt' = t'₁ - t'₀ = 0.28867 - (-0.57735) = 0.866 seconds in frame S'.

You can now see that the time dilation factor is still the same (0.866 seconds in S' for every second in S or a time dilation factor of 1/0.866 = 1.1547) despite the clock being further away.

Note that two calculations done above to calculate the coordinates of the events and then subtracting them to get the difference interval can be done a single calculation as:

Δt' = γ(Δt - Δx * v/c²) = 1.1547( 1 - 0.5*0.5) = 0.866s.

While the Lorentz transformation can be used to calculate transformed intervals and instantaneous coordinates, the time dilation formula can only be used with intervals. In other words the time dilation formula can tell you that one clock is running slower than another by a factor of 1.1547 but it cannot tell you that when a clock in S is reading 3PM that a clock in S' is reading 2PM, whereas the Lorentz transformation can.

In the scenario described in this thread, since the clocks were synchronized to zero at the origins of the two rest frames, we can use the time dilation formula to show the relationship between the Proper Time on either clock to its Coordinate Time. I made it very clear in my descriptions that the calculations applied only to this scenario. In my last post I made the point that the incremental version of the time dilation formula is usually more useful because it can be applied in any scenario, not just the one that we have been discussing so far.

 

[yuiop]

Usually, when we set the origins of two frames to coincide, we also synchronize the two clocks to zero at that event. I don't see where you synchronized the two clocks in your new example. Until you do that, I don't see how you can just say the spaceship clock had some reading on it at some location distant from the planet clock.

I did set the two clocks at the origins of the two frames to be zero at the time the origins coincide. It is contained in the statement "This is using the convention that the origins of the frames coincided at x=0, t=0, x'=0 and t'=0.". Although I did not state it, it is usually assumed that all clocks that are at rest in a given inertial reference frame that are used to determine time coordinates in that irf, are synchronised with each other. Given that information, we can determine the time t' and location x' in S' for any event t and x in S.

Second, you are using the word "event" differently than I have ever heard anyone use it in a discussion about relativity. Could you please define what you mean by "event"?

I am not sure what you find so unusual in my use of event. Could you elaborate? As far as I am concerned an event is uniquely defined as a time coordinate and three spatial coordinates in a given inertial reference frame. In a different inertial reference frame the coordinates of the same event are different from the first irf, but but they are related by the Lorentz transformations.

I don't see why we need this array of observers. Maybe you should explain exactly where they are located and exactly what they see and exactly when they see it.

You do not "need" an array of observers, but it is convenient that if there happens to be an observer adjacent to the event that is at rest in a given irf and that has a clock synchronised with a clock at the origin of the irf, then whatever the reading on that observers clock is exactly what is predicted by the Lorentz transformations without taking light travel times into account.

First, you are using the word "see" differently than I have been using it in this thread. "See" means what you observe with your eyes and that's not what you mean here. Could you please define what you mean by "see"?

Given that I am using observers that are local to the events that are being analysed, there are no issues with light travel times so "see" and measured can be used interchangeably when we are talking about local time or spatial coordinates. Yes, there could be an issue with Doppler effects but that was not originally part of the original thread.

 

[ghwellsjr]

Usually, when we set the origins of two frames to coincide, we also synchronize the two clocks to zero at that event. I don't see where you synchronized the two clocks in your new example. Until you do that, I don't see how you can just say the spaceship clock had some reading on it at some location distant from the planet clock.

I did set the two clocks at the origins of the two frames to be zero at the time the origins coincide. It is contained in the statement "This is using the convention that the origins of the frames coincided at x=0, t=0, x'=0 and t'=0.". Although I did not state it, it is usually assumed that all clocks that are at rest in a given inertial reference frame that are used to determine time coordinates in that irf, are synchronised with each other. Given that information, we can determine the time t' and location x' in S' for any event t and x in S.

I did not know about this assumption. I didn't even know that clocks are used to determine time coordinates. I had no idea that when the OP set up this scenario in post #4 with two clocks, one on a planet and one on a spaceship passing by at 0.5c that those two clocks were being used to determine time coordinates. I thought coordinates were independent of any observers or clocks that are described by those coordinates. That's why I went into great detail in post #7 to specify all these things. I didn't know I could have just assumed them.

Can you point me to an authoritative online reference that supports your assumption?

Second, you are using the word "event" differently than I have ever heard anyone use it in a discussion about relativity. Could you please define what you mean by "event"?

I am not sure what you find so unusual in my use of event. Could you elaborate? As far as I am concerned an event is uniquely defined as a time coordinate and three spatial coordinates in a given inertial reference frame. In a different inertial reference frame the coordinates of the same event are different from the first irf, but but they are related by the Lorentz transformations.

Yes, that is a good definition of "event".

Here's what you said about the first "event":

It means that both the planet observer and the spaceship observer see 1 second indicated on the planet clock and 0.866s on the spaceship clock at the same event if they are both momentarily alongside the event and each other, but their clocks read differently because they are ticking at different rates in any given reference frame.

This "event" occurs at the coordinate time in the planet's rest frame of 1 second when the planet and the spaceship are separated by 0.5 light-seconds and yet you said they are both momentarily alongside the event and each other. It appears that you are considering the line of simultaneity at 1 second to be one "event".

Here's what you said about the second "event":

At the later event, if both observers are at the same event alongside each other, then both observers see 1.1547 seconds on the planet clock and 1 second on the spaceship clock.

This "event" occurs at the coordinate time in the planet's rest frame of 1.1547 seconds when the planet and the spaceship are separated by 0.577 light-seconds and yet you again said they are both alongside each other. Again it appears that you are considering the line of simultaneity at 1.1547 second to be one "event".

I guess I must have misunderstood what you meant but even after reading your correct definition of an event, I still have no idea what you must have meant. Maybe you could reword it.

I don't see why we need this array of observers. Maybe you should explain exactly where they are located and exactly what they see and exactly when they see it.

You do not "need" an array of observers, but it is convenient that if there happens to be an observer adjacent to the event that is at rest in a given irf and that has a clock synchronised with a clock at the origin of the irf, then whatever the reading on that observers clock is exactly what is predicted by the Lorentz transformations without taking light travel times into account.

I'm glad you changed your mind. Let me make sure I understand your new position: we don't need any observers with synchronized clocks, the Lorentz transformations are sufficient, correct?

First, you are using the word "see" differently than I have been using it in this thread. "See" means what you observe with your eyes and that's not what you mean here. Could you please define what you mean by "see"?

Given that I am using observers that are local to the events that are being analysed, there are no issues with light travel times so "see" and measured can be used interchangeably when we are talking about local time or spatial coordinates. Yes, there could be an issue with Doppler effects but that was not originally part of the original thread.

Have you change your mind back again?

And what issues are there with Doppler effects? I didn't know there were any.