- 22,169
- 3,327
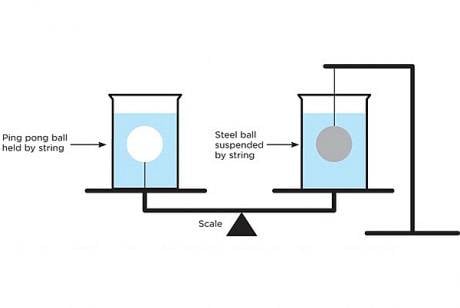
What will happen to the balance:
 )
)micromass said:What will happen
D H said:Way to go Zeta!
There apparently are a lot of people here who think they can pick themselves up by their bootstraps.
BobKat said:It boils down to this question: Does the upward force caused by the air inside the ping pong ball counterbalance the added weight of the ping pong ball itself and the string which holds it. Both balls displace the same amount of water (presumably) and the ball on the right adds no weight to the right side. I suspect the scale stays even, because the air lifts the ball and string - BUT the string is attached to the bottom of the glass, so I don't think it can lift the glass by its own bootstrap (string).
BobKat said:Guess I don't understand how the steel ball contributes the weight of its volume in water to the weight on the right...
BobKat said:Guess I don't understand how the steel ball contributes the weight of its volume in water to the weight on the right...
"easiest to think of it..."? I did not understand one word of what you said. And their weights (including the balls in them) are not the same.chingel said:I think it is easiest to think of it in terms of external forces on the containers, since their weights are the same. The pressure of the water depends only the the height of the water level, which is the same for both of them, but the left container has an additional string pulling it up.
I think we have to be careful not to say that the steel ball's weight somehow channels through the water, because the water pressure is the same in both containers.
Gerinski said:"easiest to think of it..."? I did not understand one word of what you said. And their weights (including the balls in them) are not the same.
The buoyant force on each ball is the same. Buoyant force depends only on the volume of fluid displaced, not the mass of the ball itself.derek10 said:I still don't get it:
Why does the steel ball have buoyancy and the ping pong one doesn't? is it because the steel one is more massive than the other?
(BTW I though than the balance would lean to the left due to the extra weight of the ping pong ball)
Doc Al said:The buoyant force on each ball is the same. Buoyant force depends only on the volume of fluid displaced, not the mass of the ball itself.
Extra weight of the ping pong ball?
That was my first idea too. And it seems like the simplest argument so far to me.chingel said:Water pressure on both of the containers is exactly the same everywhere, but the left container has an extra string attached to it pulling it up, therefore it will go up.
You have two identical steel balls hanging on opposite sides of a scale like this:

You have two buckets, one with water and one with glycerin, standing on opposite sides of a scale like this:
Both scales are initially balanced. Then you fully submerge the balls into the buckets without touching the walls.
Does the balance of the scales change? If yes, how?
A.T. said:Here is a similar one:
I don't thing that's correct, the string in the left container is not pulling it up, as someone said "nobody can lift himself by pulling his bootstraps".chingel said:View the container itself as a system, viewing everything inside and outside of it as external. The containers themselves are the same, they weigh the same. Water pressure on both of the containers is exactly the same everywhere, but the left container has an extra string attached to it pulling it up, therefore it will go up.
As both balls have the same volume and are completely submerged, they both have the same upward buoyant force.Gerinski said:I see the buoyancy argument but as Derek I do not see why only the right side should have the weight of the steel ball's buoyancy and not the left side the same buoyancy by the volume of water displaced by the ping-pong ball.
The balls are held in some fully submerged position, not just dropped and resting on the bottom. So other forces are involved.derek10 said:No it won't change, both sides of the scale have the same mass/weight
Thats the first thing I thought so I'm pretty sure I'm wrong
Doc Al said:The balls are held in some fully submerged position, not just dropped and resting on the bottom. So other forces are involved.
Gerinski said:I don't thing that's correct, the string in the left container is not pulling it up, as someone said "nobody can lift himself by pulling his bootstraps".
I see the buoyancy argument but as Derek I do not see why only the right side should have the weight of the steel ball's buoyancy and not the left side the same buoyancy by the volume of water displaced by the ping-pong ball.
That's weird to hear from you as one of your previous posts says:Doc Al said:As both balls have the same volume and are completely submerged, they both have the same upward buoyant force.
It get's lighter. Suppose we put two flasks on the scale, each containing a ping pong ball anchored from below. The scale will balance because we're measuring two identical systems. Now cut the string on the right. The ping pong ball will float, with almost all of the ball out of the water. The air will buoy the part of the ball that is sticking out of the water. The air in the ball (about 4 centigram) will be a part of what is measured on the left. On the right, that air won't register. The scale will tilt down to the left.chingel said:If we cut the string on the left container and let the ball float, the whole container doesn't get any heavier ...
That analysis is not quite correct. There is a difference between a floating ping pong ball and a submerged one. The submerged ping pong ball system includes the mass of the air inside the ping pong ball. The floating ping pong ball, most of that mass is buoyed by the air. The difference is about 4.3 milligrams.micromass said:Here is the experiment with the final answer:
https://www.youtube.com/watch?v=b_8LFhakQAk
D H said:That analysis is not quite correct. There is a difference between a floating ping pong ball and a submerged one. The submerged ping pong ball system includes the mass of the air inside the ping pong ball. The floating ping pong ball, most of that mass is buoyed by the air. The difference is about 4.3 milligrams.
That said, a lab balance scale that's holding two flasks each containing about a liter of water most likely isn't going to be sensitive to that 4.3 milligram difference.
D H said:It get's lighter. Suppose we put two flasks on the scale, each containing a ping pong ball anchored from below. The scale will balance because we're measuring two identical systems. Now cut the string on the right. The ping pong ball will float, with almost all of the ball out of the water. The air will buoy the part of the ball that is sticking out of the water. The air in the ball (about 4 centigram) will be a part of what is measured on the left. On the right, that air won't register. The scale will tilt down to the left.
The way he's measuring he can't sense a 4.3 centigram difference. 4.3 centigrams is 0.43 milliliters of water. His method of filling the containers with water has to yield an experimental error that is well over that.micromass said:Well, here you go:
We can eliminate that buoyant force by the air on the containers by putting a small amount of water in the trays and then put the flasks on those trays.chingel said:Wouldn't air also buoy the higher water level that is in the container with the ball submerged? If both of the systems had the same volume they would be buoyed by the same amount, neglecting change of density with height.
D H said:That analysis is not quite correct. There is a difference between a floating ping pong ball and a submerged one. The submerged ping pong ball system includes the mass of the air inside the ping pong ball. The floating ping pong ball, most of that mass is buoyed by the air. The difference is about 4.3 milligrams.
That said, a lab balance scale that's holding two flasks each containing about a liter of water most likely isn't going to be sensitive to that 4.3 milligram difference.
D H said:We can eliminate that buoyant force by the air on the containers by putting a small amount of water in the trays and then put the flasks on those trays.
chingel said:Wouldn't air also buoy the higher water level that is in the container with the ball submerged? If both of the systems had the same volume they would be buoyed by the same amount, neglecting change of density with height.
We can eliminate that buoyant force by the air on the containers by putting a small amount of water in the trays and then put the flasks on those trays.
sophiecentaur said:I don't quite go along with that. The volume of the pingpong ball is still displacing the same amount of air, whether it's out in the air or displacing it via the water displacement. So why isn't it experiencing the same amount of upthrust in both positions?
chingel said:I'm not clear on what exactly do you do with the flasks and the water and how would that eliminate the buoyant force? I would think that two systems with equal volume would still experience the same buoyant force if the air density is the same.
Think of how your toilet works. Toggling the handle lifts the flapper valve off its seat. The flapper valve is less dense than water, so it remains buoyed off the seat until the water level drops below the valve. The valve settles back in place at this point, sealing the tank. The tank starts to fill with water. The pressure from the water seals the valve even more firmly in place.AlephZero said:Sorry, I don't understand what you are doing there, without a diagram or some equations. Putting the same amount of water on each tray wouldn't seem to affect anything.
D H said:Think of how your toilet works. Toggling the handle lifts the flapper valve off its seat. The flapper valve is less dense than water, so it remains buoyed off the seat until the water level drops below the valve. The valve settles back in place at this point, sealing the tank. The tank starts to fill with water. The pressure from the water seals the valve even more firmly in place.
The flapper valve is less dense than water. So why doesn't the water buoy the valve up, making the toilet run and run and run? The answer is that by sealing itself in place, the flapper valve stops buoyancy in its tracks. Once sealed, the forces on the flapper valve are the weight of the valve, the water pressure from above, and the air pressure from below. The net downward force is stronger than gravity alone. Once the tank fills, that valve is held firmly in place by the pressure differential until the next time the toilet valve is toggled. There is no buoyant force to lift the flapper valve off the seat until then.I'm doing the same thing here with water in the trays that hold the flasks. The water keeps air from getting under the flask and thereby stops atmospheric buoyancy on the flasks in its tracks.
3.35E-05 m^3 volume of a ping pong ball
12 N/m^3 of air
0.000402 Newtons
102 grams/N
0.041004 grams of airmicromass said:Well, here you go:
https://www.youtube.com/watch?v=7ADBL7_A9qA
You have two identical steel balls hanging on opposite sides of a scale like this:

You have two buckets, one with water and one with glycerin, standing on opposite sides of a scale like this:
Both scales are initially balanced. Then you fully submerge the balls into the buckets without touching the walls.
Does the balance of the scales change? If yes, how?
But both scales are initially in balance, so the weight of both fluids is the same.derek10 said:Then I think the glycerin one will weight more as glycerin is denser than water
D H said:Think of how your toilet works. Toggling the handle lifts the flapper valve off its seat. The flapper valve is less dense than water, so it remains buoyed off the seat until the water level drops below the valve. The valve settles back in place at this point, sealing the tank. The tank starts to fill with water. The pressure from the water seals the valve even more firmly in place.
The flapper valve is less dense than water. So why doesn't the water buoy the valve up, making the toilet run and run and run? The answer is that by sealing itself in place, the flapper valve stops buoyancy in its tracks. Once sealed, the forces on the flapper valve are the weight of the valve, the water pressure from above, and the air pressure from below. The net downward force is stronger than gravity alone. Once the tank fills, that valve is held firmly in place by the pressure differential until the next time the toilet valve is toggled. There is no buoyant force to lift the flapper valve off the seat until then.I'm doing the same thing here with water in the trays that hold the flasks. The water keeps air from getting under the flask and thereby stops atmospheric buoyancy on the flasks in its tracks.