Tensors Definition and 376 Threads
-

Undergrad Transformation of second rank tensor
In all the sources I checked, except for one by Dwight E. Neuenschwander, Tensor Calculus for Physics: A Concise Guide, they only provide the definition of a tensor (or describe how it transforms). However, Neuenschwander attempts to motivate the definition of a second-rank tensor. First, he...- LightPhoton
- Thread
- Coordinate transformations Tensor analysis Tensors
- Replies: 4
- Forum: Differential Geometry
-

Undergrad How Can Tensors Be Evaluated to Scalars?
Many descriptions of tensors define them to be these kind of multidimensional arrays of numbers, as generalizations of vectors and matrices, that transform in a certain way. But, mathematically, tensors are functions whose domains are these multidimensional arrays and whose codomains/ranges are...- LarryS
- Thread
- Scalars Tensors
- Replies: 4
- Forum: Special and General Relativity
-

Undergrad Symbol for matrix representative of a tensor
Hi, I'm simply searching for some standard symbol (in place of an equals sign) to indicate that a matrix is a representative of a tensor in some given basis. Is there any standardized symbol like this, or how is this usually written in literature? E.g. say we have a O(1,1) metric tensor gμν...- doktorglas
- Thread
- Matrices Notation Tensors
- Replies: 5
- Forum: Linear and Abstract Algebra
-
W
Undergrad Question about Cartesian Tensors
I am not a mathematician but an Engineer-in-Training studying mechanics. That being said why does equation I-10 equal 1 when k equals i and 0 when k does not equal i?- Worn_Out_Tools
- Thread
- Engineering Mechanics Tensors
- Replies: 3
- Forum: Calculus
-

Integrals of isotropic tensors, for expansion over spherical harmonics
Consider an expansion for the density ##\rho(t,\mathbf{x})## of the form$$\rho(t,\mathbf{x}) = \sum_{l=0}^{\infty} a_{i_1 i_2 \dots i_{\mathscr{l}}}(t,r) \hat{x}_{i_1} \hat{x}_{i_2} \dots \hat{x}_{i_{\mathscr{l}}}$$where ##r = |\mathbf{x}|## and ##\hat{x}_i = x_i/r##. Also, ##a_{i_1 i_2 \dots...- ergospherical
- Thread
- Isotropic Spherical Tensors
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

What are Good Books on Tensors for Understanding Einstein's Field Equation?
I'm looking for good books on Tensors. I have "Introduction to Tensor Analysis and the Calculus of Moving Surfaces" from Pavel Grinfeld. But i look for others. [Mentor Note: Thread moved from the Relativity forum]- Alaindevos
- Thread
- Books Calculus Tensors
- Replies: 33
- Forum: Science and Math Textbooks
-
What's a Tensor?
A brief explanation of vector and tensor concepts from A Student's Guide to Vectors and Tensors by Dan Fleisch. I found this when I was trying to better understand tensors and how they are used.- scottdave
- Media item
- Tensor algebra Tensors
- Comments: 0
- Category: Linear Algebra
-

Advanced elasticity book recommendation
TL;DR Summary: Pretty much confused about an advanced elasticity book.Resource recommendation is asked. My last semester in freshman year of bs physics included a chapter on elasticity,it was not at the advanced level and by advanced level i mean atleast the tensor stuff.Well,I want to read...- rajsekharnath
- Thread
- Books Elasticity Tensors
- Replies: 4
- Forum: Science and Math Textbooks
-

Solving a Problem with Interchanging Field Tensors
Exercise: Solution: The result is correct, but I'm unsure about equation from 29 to 30 where right-hand side became just the covariant dual field tensor. I assumed that I could interchange the covariant dual- and normal covariant field tensor, but don't think it's possible since matrices...- milkism
- Thread
- Electromagnatism Field Special relativity Tensors
- Replies: 5
- Forum: Advanced Physics Homework Help
-
K
Undergrad Tensor decomposition, Sym representations and irreps.
New to group theory. I have 3 questions: 1. Tensor decomposition into Tab = T[ab] +T(traceless){ab} + Tr(T{ab}) leads to invariant subspaces. Is this enough to imply these subreps are irreducible? 2. The Symn representations of a group are irreps. Why? 3. What is the connection between...- knowwhatyoudontknow
- Thread
- Decomposition Representation theory Representations Tensor Tensors
- Replies: 1
- Forum: Linear and Abstract Algebra
-

High School Attempted proof of the Contracted Bianchi Identity
My Attempted Proof ##R^{mn}_{;n} - \frac {1} {2} g^{mn} R_{;n} = 0## ##R^{mn}_{;n} = \frac {1} {2} g^{mn} R_{;n}## So, we want ##2 R^{mn}_{;n} = g^{mn} R_{;n} ## Start w/ 2nd Bianchi Identity ##R_{abmn;l} + R_{ablm;n} + R_{abnl;m} = 0## Sum w/ inverse metric tensor twice ##g^{bn} g^{am}...- Vanilla Gorilla
- Thread
- Curvature tensor Identity Proof Tensor Tensor algebra Tensor calculus Tensors
- Replies: 1
- Forum: Differential Geometry
-
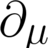
How to show that this expression with tensors reduces to zero?
I simply just wrote down the definition of ##\Gamma'^a_{bc}##, and inserted the transformations of ##g'^{ad}##, ##g'_{dc,b}##, and the like terms. After some rearranging and cancelling out, $$\Gamma'^a_{bc}=\frac{\partial x'^a}{\partial x^e}\frac{\partial x^f}{\partial x'^b}\frac{\partial...- phyTens
- Thread
- Expression Tensors Zero
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
D
Undergrad Understanding tensor product and direct sum
Hi, I'm struggling with understanding the idea of tensor product and direct sum beyond the very basics. I know that direct sum of 2 vectors basically stacks one on top of another - I don't understand more than this . For tensor product I know that for a product of 2 matrices A and B the tensor...- dwd40physics
- Thread
- Direct sum Product Sum Tensor Tensor product Tensors total angular momentum
- Replies: 11
- Forum: Quantum Physics
-

Graduate Decomposing Rank-2 Tensors in Dirac's "General Theory of Relativity
Dirac's book "General Theory of Relativity" says on p. 2 that a general rank-2 tensor can be written as a sum of outer products: $$ T^{\mu\nu} = A^\mu B^\nu + A'^\mu B'^\nu + A''^\mu B''^\nu + \cdots $$ Importantly, he repeats this on p. 18, in developing the covariant derivative, where he...- Kostik
- Thread
- Tensors
- Replies: 5
- Forum: Special and General Relativity
-

Undergrad Dirac Notation for Vectors and Tensors (Neuenschwander's text ....)
I am reading Tensor Calculus for Physics by Dwight E. Neuenschwander and am having difficulties in confidently interpreting his use of Dirac Notation in Section 1.9 ... in Section 1.9 we read the following: I need some help to confidently interpret and proceed with Neuenschwander's notation...- Math Amateur
- Thread
- Dirac Dirac notation Notation Tensors Text Vectors
- Replies: 16
- Forum: Differential Geometry
-
SH2372 General Relativity (6): Type (N,M) tensors
- Orodruin
- Media item
- Tensors
- Comments: 0
- Category: Relativity
-
SH2372 General Relativity (5): Type (0,M) tensors
- Orodruin
- Media item
- Tensors
- Comments: 0
- Category: Relativity
-

Is there a mistake in this tensor multiplication problem?
ep_{ijkl} M^{ij} N^{kl} + ep_{ijkl}N^{ij} M^{kl} The second term can be rewritten with indices swapped ep_{klij} N^{kl}M^{ij} Shuffle indices around in epsilon ep{klij} = ep{ijkl} Therefore the expression becomes 2ep_{ijkl}M^{ij}N^{kl} Not zero. What is wrong here?- DuckAmuck
- Thread
- Multiplication Tensor Tensors
- Replies: 5
- Forum: Advanced Physics Homework Help
-

Undergrad Calculate Eigenvalues of Electromagnetic & Stress-Energy Tensors
How can we (as nicely as possible... i.e. not via characteristic polynomial) calculate the eigenvalues of ##F_{ab} = \partial_a A_b -\partial_b A_a## and ##T_{ab} = F_{ac} {F_b}^c- (1/4) \eta_{ab} F^2 ## and what is their physical meaning?- ergospherical
- Thread
- Eigenvalues Electromagnetic Tensors
- Replies: 3
- Forum: Special and General Relativity
-
E
Undergrad How can the dual tensors derivation be achieved using rotation matrices?
Hello, I'm reading Group Theory in a nutshell for physicist by A Zee. When he introduced Dual tensors (pp 192), he made a claim with a light hint, and I have had great trouble deriving this claim, any help would be appreciated - Let ##R \in SO(N)## be an ##N##-dimensional rotation, then the...- euphoricrhino
- Thread
- Derivation Dual Tensors
- Replies: 5
- Forum: Linear and Abstract Algebra
-

Does anyone know which are Ricci and Riemann Tensors of FRW metric?
I just need to compare my results of the Ricci and Riemann Tensors of FRW metric, but only considering the spatial coordinates.- physicsuniverse02
- Thread
- Frw metric General relativity Metric Ricci tensor Riemann Riemann tensor Tensors
- Replies: 2
- Forum: Advanced Physics Homework Help
-
S
Books/resources for exercises on tensors and multilinear algebra
I'm self-studying tensors from a book that doesn't have exercises. The book is Semi-Riemannian Geometry by Newman. To get a better feel for index manipulation, tensor results and calculations, I'm looking for a book that has many exercises in these topics. I'd be grateful if those knowledgeable...- Shirish
- Thread
- Algebra Exercises Tensors
- Replies: 6
- Forum: Science and Math Textbooks
-
G
Graduate Understand (k,l) Tensors in Gen. Relativity
In both Wald and Carroll, a type (k,l) tensor has k dual vectors and l vectors, yet a (1,0) tensor is a vector and a (0,1) tensor is a dual vector. I must be missing something simple. Please explain.- GeoffFB
- Thread
- General General relativity One-forms Relativity Tensors Vectors
- Replies: 7
- Forum: Special and General Relativity
-

Undergrad Understanding Tensors & Knot Theory in Physics
Hello everyone! I'm currently self studying knot theory and I am at the point where I am looking at its relationship with other fields. I am a math and physics student, but my physics understanding is far behind my understanding of math. Hence, I would really like some help interpreting some...- lekh2003
- Thread
- Tensors
- Replies: 4
- Forum: Beyond the Standard Models
-

Undergrad Learn Physics with Eigenchris: Relativity & Tensors
This set of videos by eigenchris (separate playlists on Relativity and on Tensors) also looks interesting and can help anyone interested in learning about these topics. A while back I watched some of them and thought they could be helpful. I like his presentation of one-forms. (I've been...- robphy
- Thread
- Relativity Tensors Videos
- Replies: 12
- Forum: Special and General Relativity
-
U
How to prove ##V_{ai;j}=V_{aj;i}## in curved space using the given equation?
Question ##1##. Consider the following identity \begin{equation} \epsilon^{ij}_{\phantom{ij}k}\epsilon_{i}^{\phantom{i}lm}=h^{jl}h^{m}_{\phantom{m}k}-h^{jm}h^{l}_{\phantom{l}k} \end{equation} which we know holds in flat space. Does this identity still hold in curved space? and if so, how...- user1139
- Thread
- General relaivity Tensor calculus Tensors
- Replies: 3
- Forum: Advanced Physics Homework Help
-
A
Dependence of the stress vector on surface orientation
According to Cauchy's stress theorem, the stress vector ##\mathbf{T}^{(\mathbf{n})}## at any point P in a continuum medium associated with a plane with normal unit vector n can be expressed as a function of the stress vectors on the planes perpendicular to the coordinate axes, i.e., in terms of...- AndersF
- Thread
- Cauchy stress Fluid dynamics Orientation Stress Stress tensor Surface Tensors Vector
- Replies: 4
- Forum: Advanced Physics Homework Help
-

Undergrad Proving Lorentz Metric on Real Type (1,0;1,0) Tensors in Wald Ch. 13
In ch. 13, pg.349 of Wald it's asked to prove that ##g_{AA'BB'} = \epsilon_{AB} \bar{\epsilon}_{A'B'}## is a Lorentz metric on ##V## (containing the real elements of the vector space ##Y## of type ##(1,0;1,0)## tensors). Given the basis ##t^{AA'} = \dfrac{1}{\sqrt{2}}(o^A \bar{o}^{A'} + \iota^A...- ergospherical
- Thread
- Lorentz Metric Tensors Type
- Replies: 2
- Forum: Special and General Relativity
-
A
Undergrad Expressing Vectors of Dual Basis w/Metric Tensor
I'm trying to understand why it is possible to express vectors ##\mathbf{e}^i## of the dual basis in terms of the vectors ##\mathbf{e}_j## of the original basis through the dual metric tensor ##g^{ij}##, and vice versa, in these ways: ##\mathbf{e}^i=g^{ij}\mathbf{e}_j##...- AndersF
- Thread
- Basis Dual Dual basis Metric Metric tensor Tensor Tensor algebra Tensor notation Tensors Vectors
- Replies: 8
- Forum: Special and General Relativity
-
G
Undergrad The tensor product of tensors confusion
> **Exercise.** Let T1and T2be tensors of type (r1 s1)and (r2 s2) respectively on a vector space V. Show that T1⊗ T2can be viewed as an (r1+r2 s1+s2)tensor, so that the > tensor product of two tensors is again a tensor, justifying the > nomenclature... What I’m reading:《An introduction to...- GR191511
- Thread
- Confusion Product Tensor Tensor product Tensors
- Replies: 32
- Forum: Linear and Abstract Algebra
-

Graduate Calculating Lie Derivatives for Tensors & Vectors
I am writing a code to calculate the Lie Derivatives, and so far, I have defined the Covariant derivative 1) for scalar function; $$\nabla_a\phi \equiv \partial_a\phi~~(1)$$ 2) for vectors; $$\nabla_bV^a = \partial_bV^a + \Gamma^a_{bc}V^c~~(2)$$ $$\nabla_cV_a = \partial_cV_a -...- Arman777
- Thread
- Derivative Lie derivative Tensors Vectors
- Replies: 11
- Forum: Special and General Relativity
-
I
Geometry Geometrical books (differential geometry, tensors, variational mech.)
I am looking for math books that focus on geometrical interpretations. Sadly most of the modern books lack these interpretations and only consists out of theorems and proofs. It seems to me that most modern mathematicians are pure left-brain sequential thinkers that do not have a lot of...- Idun
- Thread
- Books Differential geometry Geometrical Geometry Tensors
- Replies: 2
- Forum: Science and Math Textbooks
-

Understanding Tensors: Is Misner Thorne and Wheeler Enough?
Summary:: Does the textbook Misner Thorne and Wheeler have all I need to understand tensors in order to learn GR? Does the textbook Misner Thorne and Wheeler have all I need to understand tensors in order to learn GR? I have that textbook but never went through it. Tensors greatly intimidate...- bob012345
- Thread
- Tensors Wheeler
- Replies: 60
- Forum: Science and Math Textbooks
-

Geometry "The Geometry of Physics" - Theodore Frankel
Hello everyone. I was browsing through Amazon and found the aforementioned book by Theodore Frankel. As it is available at a relatively cheap price and covers a TON of material I was considering buying it for future use . Although the author says the prerequisites are only multivariable...- Falgun
- Thread
- Geometry Physics Tensors
- Replies: 6
- Forum: Science and Math Textbooks
-
U
Clarification on electric quadrupole moment definition
I have encountered two (?) definitions of the electric quadrupole moment. They are: $$Q_{ij}=\frac{1}{2}\int \rho(\vec{x}')x'_i x'_j\,\mathrm{d}^3x'$$ and $$Q_{ij}=\int (3x'_i x'_j-\delta_{ij}x'^2)\rho(\vec{x}')\,\mathrm{d}^3x'$$ I am trying to study radiation arising from the electric...- user1139
- Thread
- Definition Electric Electromagnetism Moment Radiation Tensors
- Replies: 5
- Forum: Advanced Physics Homework Help
-
R
Prove that If A,B are 3x3 tensors, then the matrix C=AB is also a tensor
I try to solve but i have 1 step in the solution that I don't understand who to solve. Below in the attach files you can see my solution, the step that I didn't make to prove Marked with a question mark. thanks for your helps (:- ReuvenD10
- Thread
- 3x3 Matrix Tensor Tensors
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Insights The Electric Field Seen by an Observer: A Relativistic Calculation with Tensors
Continue reading...- robphy
- Thread
- Calculation Electric Electric field Field Observer Relativistic Tensors
- Replies: 1
- Forum: Special and General Relativity
-
V
Graduate Analysis of a Frictional Contact Problem with Adhesion
Hi, I'd to work with a model which represents a contact problem. I want to suppose that f_0=0 and f_2=0 where f_0 is a density of body forces and f_2 is a density of surface tractions . I am mathematician so I don't know if the hypothesis that I'd to suppose will make the problem have a sense in... -
U
Help with Tensors: Using Einstein Summation Convention
Assuming Einstein summation convention, suppose $$R^2=\eta_{\mu\nu}x^{\mu}x^{\nu}$$ I was able to show that $$\partial_{\mu}R=\frac{\eta_{\mu\nu} x^{\nu}}{R}$$ by explicitly doing the covariant component of the four-gradient and using the kronecker tensor. However, how do I use the equation...- user1139
- Thread
- Special relativity Tensor calculus Tensors
- Replies: 6
- Forum: Advanced Physics Homework Help
-

Geometry Calculations with tensors in modern notation
Is there a book that emphasizes performing calculations with tensors in modern notation?- Frabjous
- Thread
- Calculations Notation Tensors
- Replies: 5
- Forum: Science and Math Textbooks
-
K
Graduate Can we always rewrite a Tensor as a differential form?
I read in the book Gravitation by Wheeler that "Any tensor can be completely symmetrized or antisymmetrized with an appropriate linear combination of itself and it's transpose (see page 83; also this is an exercise on page 86 Exercise 3.12). And in Topology, Geometry and Physics by Michio...- kay bei
- Thread
- Differential Differential form Differential forms Differential geometry Form Physics textbook Tensor Tensors
- Replies: 8
- Forum: Differential Geometry
-
K
Graduate Differential Forms or Tensors for Theoretical Physics Today
There are a few different textbooks out there on differential geometry geared towards physics applications and also theoretical physics books which use a geometric approach. Yet they use different approaches sometimes. For example kip thrones book “modern classical physics” uses a tensor...- kay bei
- Thread
- Differential Differential forms Differential geometry Forms Geometric Physics Tensor Tensors Textbook Theoretical Theoretical physics
- Replies: 70
- Forum: Differential Geometry
-

Undergrad Need help with tensors and group theory
I am reading Group Theory in a Nutshell for Physicists by A. Zee. I have big problems when learning chapter IV.1 Tensors and Representations of the Rotation Groups SO(N). It reads I can understand why ##D\left ( R \right )## is a representation of SO(3), but I hardly can see why the tensor T...- Haorong Wu
- Thread
- Group Group theory Tensors Theory
- Replies: 6
- Forum: Linear and Abstract Algebra
-
Levi-Civita symbol and its effect on anti-symmetric rank two tensors
I am trying to understand the following: $$ \epsilon^{mni} \epsilon^{pqj} (S^{mq}\delta^{np} - S^{nq}\delta^{mp} + S^{np}\delta^{mq} - S^{mp}\delta^{nq}) = -\epsilon^{mni} \epsilon^{pqj}S^{nq}\delta^{mp} $$ Where S^{ij} are Lorentz algebra elements in the Clifford algebra/gamma matrices...- Jason Bennett
- Thread
- Levi-civita rank Symbol Tensors
- Replies: 2
- Forum: Advanced Physics Homework Help
-
D
High School Tensor Contraction with Metric for Stress Energy: Explained
Can you contract any part of the stress energy tensor with the metric? Say if you had four components Tu1 and contracted that with g^u1 would that produce an invariant?- dsaun777
- Thread
- Tensors
- Replies: 20
- Forum: Special and General Relativity
-

Undergrad Wigner's Theorem That All Fields Must Be Tensors
I know in 1939 Wigner published a theorem that all fields must be tensors from a couple of books, but can't find the proof anywhere. That obviously is an important result so does anyone know where I can find the proof? Another I haven't seen the proof of is the no interaction theorem. I wish...- bhobba
- Thread
- Fields Tensors Theorem
- Replies: 1
- Forum: Beyond the Standard Models
-
S
Undergrad Transformation of the contravariant and covariant components of a tensor
I have read many GR books and many posts regarding the title of this post, but despite that, I still feel the need to clarify some things. Based on my understanding, the contravariant component of a vector transforms as, ##A'^\mu = [L]^\mu~ _\nu A^\nu## the covariant component of a vector...- shinobi20
- Thread
- Components Contravariant Covariant Special relativity Tensor Tensor algebra Tensors Transformation
- Replies: 23
- Forum: Special and General Relativity
-

Graduate Weyl transformation of connection and curvature tensors
Given a Weyl transformation of the metric ##g_{\mu\nu} \rightarrow g'_{\mu\nu} = e^{\Omega(x)} g_{\mu\nu}##, I'm trying to find the corresponding connection ##\Gamma'^{\lambda}_{\mu\nu}##, and from that ##-## via the Riemann tensor ##R'^{\lambda}_{\mu\nu\kappa}## ##-## the Ricci tensor...- Rabindranath
- Thread
- Connection Curvature Tensors Transformation Weyl
- Replies: 4
- Forum: Special and General Relativity
-
M
Undergrad Understanding Spherical Tensors & Their Applications
Hello! I came across spherical tensors, and I am a bit confused about the way they are applied. For example, Pauli matrices, can be grouped together to form a rank 1 (vector) spherical tensor as ##(\sigma_-, \sigma_z, \sigma_+)##, which are the raising operator, the z projection operator and the...- Malamala
- Thread
- Spherical Tensors
- Replies: 2
- Forum: Quantum Physics
-
S
Undergrad Finding the Error in Computing Spherical Tensor of Rank 0 Using General Formula
This should be a trivial question. I am trying to compute the spherical tensor ##T_0^{(0)} = \frac{(U_1 V_{-1} + U_{-1} V_1 - U_0 V_0)}{3}## using the general formula (Sakurai 3.11.27), but what I get is: $$ T_0^{(0)} = \sum_{q_1=-1}^1 \sum_{q_2=-1}^1 \langle 1,1;q_1,q_2|1,1;0,q\rangle...- Silicon-Based
- Thread
- Quantum mechanics rank Spherical Tensor Tensors
- Replies: 1
- Forum: Quantum Physics


