1st class lever question (I think) -- tilting antenna erection mechanism

[TymerTopCat]

I want to build a tilting wireless internet structure that is 24 feet high, with a fulcrum at 6ft. The idea is when I want to work on the device (which is 24 ft in the air), I can just unlatch the mast and tilt the structure down and work on it. I would like to have the pivot (or fulcum) at six feet high, with the remaining 18 ft at the top.

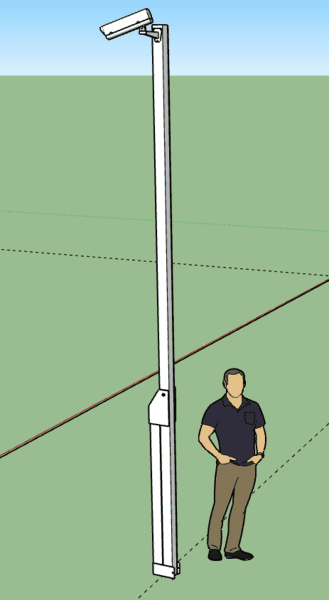
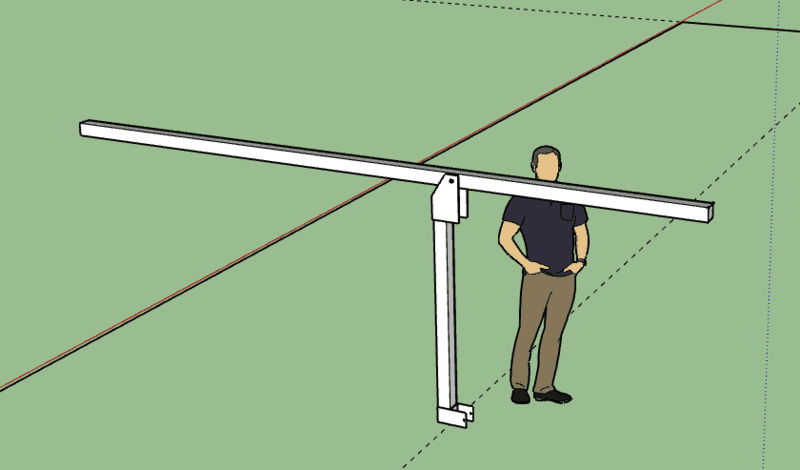
See two pictures below. One with the base up, another in horizontal position. The drawing attached is only a 15 ft version, I'm building a 24ft version which will increase the weight of the counter balance.

Question:
How much *counter weight* would I need on the short end to make the tilting operation easy on me so I don't want to use a winch, which other designs do.. I'd like it to be hand operated for simplicity. Question is how much counter weight would I need to keep the tilt operation under my control. I'm kinda fat so maybe I won't need too much counter weight.

The weight: 130lbs of Square tubing.
---------------
The support base is .125 thick, 3.5"x3.5"x24 ft long Square tubing. This tubing weighs 5.39 lbs per ft. So 24ft x 5.39 = 129.36lbs. So let's call it 130lbs. Technically there will be a small antenna on the top, about 5-10 lbs. But for now let's ignore the weight of the equipment at the top.

The pivot point or fulcrum: = 6ft from ground.
The top of the Square tubing 24ft. So there is 18feet from the fulcrum.

Thanks.
-R
Here is picture when up.

Here is another when down:

 

[AZFIREBALL]

Back of the envelope calculation.
1/4 of the weight of the pole(130/4 = 32.5 pounds) is to the right of the fulcrum.
3/4 of the weight of the pole(3/4x 130 = 97.5 pounds) is to the left of the fulcrum.

The CW moment around the fulcrum caused by the pole is approximated by summing the products of each foot of length by the weight of each foot of the pole on the right side.
Thus: (6!)(5.4) = 113 ft lbs. (6! = 1+2+3+4+5+6 = 21)

The CCW moment around the fulcrum caused by the pole is approximated by summing the products of each foot of length by the weight of each foot of the pole on the left side.
Thus: (18!)(5.4) = 926 ft lbs. (18! = sum of the digits 1 through 18 = 171).

From the above you need to add a CW moment equal to the difference between the two moments.
926 – 113 = 813 ft lbs.
If you add a weight who’s center of gravity is at the 5 foot mark, it will need to weigh
813/5 = 163 lbs. Because (163)5 = 813 ft lbs.
At the 4 foot mark it will need to be 813/4 = 203. Because (203)4 = 813 ft lbs.

Note: if you weigh at least 200 pounds you could use your own body weigh to lower the pole.

 

[TymerTopCat]

The CW moment around the fulcrum caused by the pole is approximated by summing the products of each foot of length by the weight of each foot of the pole on the right side.
Thus: (6!)(5.4) = 113 ft lbs. (6! = 1+2+3+4+5+6 = 21)

The CCW moment around the fulcrum caused by the pole is approximated by summing the products of each foot of length by the weight of each foot of the pole on the left side.
Thus: (18!)(5.4) = 926 ft lbs. (18! = sum of the digits 1 through 18 = 171).

Thank you so much for your reply.
Question #1:
What does 5.4 represent? How did you get this value?
Question #2:
Isn't (18!)(5.4) or (171*5.4) equal to 923.4 ft lbs.

I'm making a spreadsheet with these calculations. I don't want to assume anything.
-R

 

[AZFIREBALL]

5.4 is the value you provided for the weight of one foot of the pole. 130/24 = 5.4167 lbs.
(18!)(5.4167) = 926 ft lbs, (using the actual value for the weight of one foot of the pole.)

 

[TymerTopCat]

Thank you for clarifying my questions. Currently creating an excel spreadsheet to calculate different possibilities as I think I'm going to change the pole to .25 thick wall this doubles the weight of the pole, also I may consider raising the fulcrum to 8ft. The excel document will help make my decisions.

Reason, the top support steel was 1/2 inch steel and the pole was only .120. Welding 1/2 inch steel to .120 inch steel is not such a great choice and more difficult to weld because of the metal size differences. I'm a novice welder so, arc welding 1/2 steel to 1/4 inch steel much easier for me. Hence I may use 1/4 inch steel instead for the pole this is assuming I don't end up with a huge counter weight to balance it.

One thing about getting older, is that most of us get a bit wiser. For example the reason I posted this question was to build a solution to a problem that the average person suffers the consequences of, including me. Cleaning something!

So I installed surveillance cameras around my 5 acre lot, one of them is on a 23 foot Wood Power pole that I installed 2 years ago, everything works great. However! I hadn't thought about a side effect of having cameras so high up on a power pole that doesn't tilt over.
The cameras get dirty and dusty outside, so about every 2 weeks I have to clean them. And this isn't easy. First you have to drag a huge ladder to the power pole, then climb up the ladder with a towel and cleaning fluid. Doing this every 2 weeks is not fun, in fact I usually don't use the ladder. I use my Backhoe and hoist my girlfriend up in the bucket and then she cleans it. This takes two people, too hard. Time for a better solution, a tilting pole.

Thank you again for taking the time to help me clean the dust off my cameras.

-R

 

[TymerTopCat]

I think I have the formula working in excel, but values are preliminary for now.
Changes:
Post changed from .120 steel to .250 inch steel.
Length of pole: 24ft
Weight of pole: 252lbs (10.5 lbs per ft.)
Fulcrum: 6ft
Excel Calculations (Values probably rounded by excel)
================================================
171 CCW Moment 1795.5
21 CW Moment 220.5
================================================
1575 Ft Lbs (CCW-CW) Moments difference

Counter Balance Position: 6ft
Counter Balance Needed: 262.5lbs

My first attempt is to attach the counter weight to the bottom:
Using 1.0" Thick Steel places 3.5"x2ft 10 of them around ~25lbs each. (250lbs Total)
So I put 10 of them on the bottom of pole.

Since I am not a P.E. Just a software Engineer, I would guess that the added counter balance will now make the structure balance when tilted to a horizontal position 90 degrees from vertical. However, the forces to bring the pole to horizontal are probably not linear. So it would take some effort to get the pole to horizontal position. But I think this will be okay for me, I'm a pretty strong guy. After building the structure maybe I could improve the movement. I would prefer to keep the tilting of the pole simple. No hydraulics, pulleys/ winches, etc. Occam's razor right?

Thanks to AZFireball for his kindly support.

See pictures below:

And then Horizontal

https://www.physicsforums.com/Image1.gif

 

[TymerTopCat]

I suppose I could put a pull cable on the long end, to pull it down to horizontal.

If anyone has a better idea, let me know. I'll send you a picture of a brand new car or something.

-R

 

[TymerTopCat]

Here is a shot of the pivot. I can't think of anything better for now.
It uses 1/2 inch plate steel.
One inch steel pin.
Probably way over-built, but then I don't know any P.E.'s to save me from myself that would work for my wages.

 

[JBA]

The calculations are correct but the force for lowering the pole is not your problem. With the imbalance on the upper section, preventing the pole from running away and the top end crashing to the ground as the pole is swung toward the horizontal position; and, being able to raise it from that position are the issues that need to be addressed with your counterbalance.
The amount of moment is also a function of the horizontal distance of your weights from the poles vertical position as it rotates about the pivot and this applies to both the top and bottom sections of the pole. A fully counterbalanced horizontal pole will require you to provide all of the force of the moment of the upper section in its vertical position; but this can be offset by using a pulling rope long enough to increase the your distance from the pole at the start of the lowering.

 

[jrmichler]

I'm a novice welder so, arc welding 1/2 steel to 1/4 inch steel much easier for me.

I also am a novice welder, but I was able to weld a 1/16" wall thickness tube to a 1.5" thick disk:

It's not a pretty weld, but then I'm not a very good welder. The secret is to preheat the thick piece. It's the mount for my machinist vise.

I like the idea of 1/2" plate and a 1" pin for the pivot and bracket. A little overbuilt, but only a small amount of extra steel. Your offset bracket will hold it vertical, and slightly undersizing the counterweight will hold it horizontal. You still need to pin it when in the vertical position.

You have a girlfriend that's willing to ride a backhoe bucket 23 feet up? And more than once? What's your secret? Incredible riches are yours if you can teach us your secret.