omicronhuh
- 1
- 0
Good evening! I'm having trouble completing an assignment related to inelastic collisions and momentum.
Here is the statement:
You are in great shape on this hot July morning. You are working as an intern for the Montreal Police (SPVM) Collision Investigation unit. You assist the investigators in order to determine, as accurately as possible, the circumstances surrounding collisions (initial velocity of the vehicles involved, direction vehicles were heading, etc.) in order to take action against drivers at fault under the Criminal Code (dangerous driving causing death or other charges).
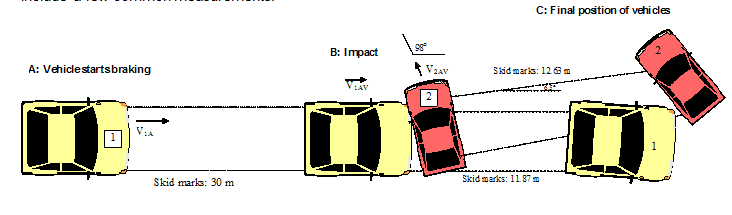
You just get to the scene of a collision involving two vehicles. The Chief Investigating Officer addresses you, “Come here quick, we need you. You know the routine, so get to work.” Your job is to take photos of the vehicles as they are positioned, and take a certain number of measurements, including the length of the skid marks and layout of the debris. You immediately draw the following sketch of the accident and include a few common measurements.Your findings are as follows:
• Numerous debris (broken glass, plastic, etc.) were found at a distance of 12.63 m from the red vehicle
• (2) and 11.87 m from the yellow vehicle (1);
• The yellow vehicle (1) seems to have braked in a straight line;
• The red vehicle (2) veered 6.5º away from its initial course;
• The marks of the impact on the red vehicle (2) show that it was heading 98º away from the yellow
• vehicle (1) at the moment of collision;
• There are skid marks over a distance of 30 m before the debris;
• The posted speed limit on this street is 70 km/h;
• Mass of vehicle 1 (yellow) 2674 kg, mass of vehicle 2 (red) 1110 kg.
I also found out that the friction coefficient of the pavement is mk = 0.86
I'll include the sketch as well:
I'm using the following velocity indicators and ignoring the ones in the sketch.
v1i = initial velocity of the yellow car
v2i = initial velocity of the red car
v1c = velocity of the yellow car just after the collision
v2c = velocity of the red car just after the collision
This are the relevant equations:
p=mv
m1v1 + m2v2 = (m1 + m2)vf
F = ma
And conservation of energy equations: U1 + K1 + Q11 = U2 + K2 + Q12
My attempts at solving this problem are as follows:
I'm starting at point c and comparing it to b to then compare b and a using momentum to solve the problem.
In my first attempt I used energy conservation to try to calculate the velocity of the cars just after the collision.
So K = Q, in this case.
1/2(m1)(v1^c)^2 + 1/2(m2)(v2c)^2 = mk(N1)(L) + mk(N2)(L)
1337v1c^2 + 555v2c^2 = 386,056.11
And I hit a roadblock, I couldn't figure out what other equations to use to get the velocity of either car right after the collision.
So, I calculated the deceleration the cars suffered thanks to the friction. I multiplied N for the friction coefficient and then divided by the mass.
a = -8.43m/s^2
Then with kinematics equations I got the velocity of the cars right after the impact.
v1c^2=-2a(x-x0)
v1c^2 = -2(-8.43)(11.87)
v1c = 14.14 m/s
v2c^2 in the x axis=-2a(x-x0)(cos 6.5)
v2c^2 = -2(-8.43)(12.63)(cos 6.5)
v2c in the x-axis = 14.54 m/s
v2c^2 in the x axis=-2a(x-x0)(sin 6.5)
v2c^2 = -2(-8.43)(12.63)(sin 6.5)
v2c in the y-axis = 4.9 m/s
And with this I try to use the momentum conservation equation:
m1v1i + m2v2i (cos 98) = m1(14.14) + m2(14.54)
2674v1i + 1110(-0.139)v2i = 53,949.76
And is at this point where I'm not sure how to proceed. I've tried using the same deceleration to know v1i with kinematics equations and then using that to know v2i, but the speed that results for the red car turns out to be quite absurd, nearing the 400km/h. I am also not sure I'm using the angles correctly.
Do you guys have any advice for me?
Thanks!
Homework Statement
Here is the statement:
You are in great shape on this hot July morning. You are working as an intern for the Montreal Police (SPVM) Collision Investigation unit. You assist the investigators in order to determine, as accurately as possible, the circumstances surrounding collisions (initial velocity of the vehicles involved, direction vehicles were heading, etc.) in order to take action against drivers at fault under the Criminal Code (dangerous driving causing death or other charges).
You just get to the scene of a collision involving two vehicles. The Chief Investigating Officer addresses you, “Come here quick, we need you. You know the routine, so get to work.” Your job is to take photos of the vehicles as they are positioned, and take a certain number of measurements, including the length of the skid marks and layout of the debris. You immediately draw the following sketch of the accident and include a few common measurements.Your findings are as follows:
• Numerous debris (broken glass, plastic, etc.) were found at a distance of 12.63 m from the red vehicle
• (2) and 11.87 m from the yellow vehicle (1);
• The yellow vehicle (1) seems to have braked in a straight line;
• The red vehicle (2) veered 6.5º away from its initial course;
• The marks of the impact on the red vehicle (2) show that it was heading 98º away from the yellow
• vehicle (1) at the moment of collision;
• There are skid marks over a distance of 30 m before the debris;
• The posted speed limit on this street is 70 km/h;
• Mass of vehicle 1 (yellow) 2674 kg, mass of vehicle 2 (red) 1110 kg.
I also found out that the friction coefficient of the pavement is mk = 0.86
I'll include the sketch as well:
I'm using the following velocity indicators and ignoring the ones in the sketch.
v1i = initial velocity of the yellow car
v2i = initial velocity of the red car
v1c = velocity of the yellow car just after the collision
v2c = velocity of the red car just after the collision
Homework Equations
This are the relevant equations:
p=mv
m1v1 + m2v2 = (m1 + m2)vf
F = ma
And conservation of energy equations: U1 + K1 + Q11 = U2 + K2 + Q12
The Attempt at a Solution
My attempts at solving this problem are as follows:
I'm starting at point c and comparing it to b to then compare b and a using momentum to solve the problem.
In my first attempt I used energy conservation to try to calculate the velocity of the cars just after the collision.
So K = Q, in this case.
1/2(m1)(v1^c)^2 + 1/2(m2)(v2c)^2 = mk(N1)(L) + mk(N2)(L)
1337v1c^2 + 555v2c^2 = 386,056.11
And I hit a roadblock, I couldn't figure out what other equations to use to get the velocity of either car right after the collision.
So, I calculated the deceleration the cars suffered thanks to the friction. I multiplied N for the friction coefficient and then divided by the mass.
a = -8.43m/s^2
Then with kinematics equations I got the velocity of the cars right after the impact.
v1c^2=-2a(x-x0)
v1c^2 = -2(-8.43)(11.87)
v1c = 14.14 m/s
v2c^2 in the x axis=-2a(x-x0)(cos 6.5)
v2c^2 = -2(-8.43)(12.63)(cos 6.5)
v2c in the x-axis = 14.54 m/s
v2c^2 in the x axis=-2a(x-x0)(sin 6.5)
v2c^2 = -2(-8.43)(12.63)(sin 6.5)
v2c in the y-axis = 4.9 m/s
And with this I try to use the momentum conservation equation:
m1v1i + m2v2i (cos 98) = m1(14.14) + m2(14.54)
2674v1i + 1110(-0.139)v2i = 53,949.76
And is at this point where I'm not sure how to proceed. I've tried using the same deceleration to know v1i with kinematics equations and then using that to know v2i, but the speed that results for the red car turns out to be quite absurd, nearing the 400km/h. I am also not sure I'm using the angles correctly.
Do you guys have any advice for me?
Thanks!