Jhenrique
- 676
- 4
In the wiki, I found this definition for the argument:
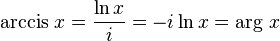
http://en.wikipedia.org/wiki/List_of_trigonometric_identities#Exponential_definitions
However, in other page of the wiki (http://en.wikipedia.org/wiki/Complex_conjugate#Use_as_a_variable), I found this definition for argument:\arg(z) = \ln(\sqrt[2 i]{z \div \bar{z} }) = \frac{ln(z) - ln(\bar{z})}{2 i}I don't understand why exist 2 defitions for the argument and how those 2 defitions are related.
http://en.wikipedia.org/wiki/List_of_trigonometric_identities#Exponential_definitions
However, in other page of the wiki (http://en.wikipedia.org/wiki/Complex_conjugate#Use_as_a_variable), I found this definition for argument:\arg(z) = \ln(\sqrt[2 i]{z \div \bar{z} }) = \frac{ln(z) - ln(\bar{z})}{2 i}I don't understand why exist 2 defitions for the argument and how those 2 defitions are related.