sl235
- 5
- 0
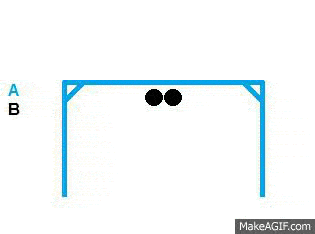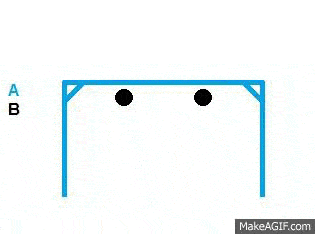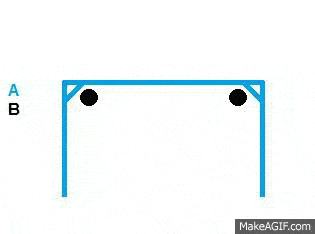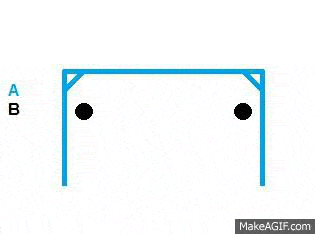
Would the 2 items displayed in the image below act as I expect in a zero G environment?
Assuming that item A had a mass of 100kg and was stationary, Items B have a mass of 1kg and travel at 10m/s.
what formula would I need to use to calculate the velocities and vectors of the items after the collision?
Thanks
Assuming that item A had a mass of 100kg and was stationary, Items B have a mass of 1kg and travel at 10m/s.
what formula would I need to use to calculate the velocities and vectors of the items after the collision?
Thanks