A 2nd Order PDE Using Similarity Method

[keropi452]

Hi All,

Does anybody know how to solve the following PDE? I tried a similarity solution method where eta = y/f(x) (which I can do successfully without the C * U term) but was unsuccessful.

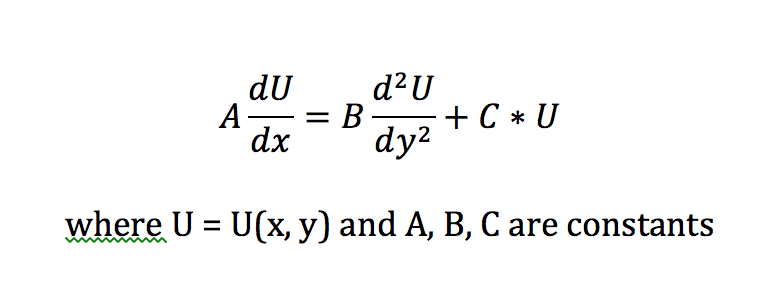
Thank you very much in advance!

 

[Ssnow]

If it is a PDE, it will be $A\frac{\partial U}{\partial x}=B\frac{\partial^2 U}{\partial y^2}+C\cdot U$ ...

 

[keropi452]

True - Sorry about that. Please take the d's to mean partial differential. Thank you for that catch.

 

[Ssnow]

If you assume that $A\not=0$ you can write your equation as $\frac{\partial U}{\partial x}=\frac{B}{A}\frac{\partial^2 U}{\partial y^2}+\frac{C}{A}\cdot U$ that is an example of diffusion reaction equation with $R(U)=\frac{C}{A}U$, seehttps://en.wikipedia.org/wiki/Reaction–diffusion_systemwhere you call $x=t$ and $y=x$, here the reaction term is simply $\frac{C}{A}U$...

Ssnow

 

[keropi452]

Thank you very much for your response and observation. Are you possibly aware of any closed form solutions to the diffusion reaction eq with R(U) = CU/A?

 

[pasmith]

The substitution u = e^{Cx/A}v results in a standard diffusion equation for v.