electrogeek
- 14
- 1
Hi everyone,
I'm struggling with the proof for the second order energy correction for perturbation theory when substituting in the first order wavefunction. I have attached an image of my current proof for it below, but I'm not sure whether this is the correct approach for it (the H's in the calculations below are hamiltonian operators)! I'm still quite new to using Dirac notation for these calculations so thought I should double-check it.
Cheers!
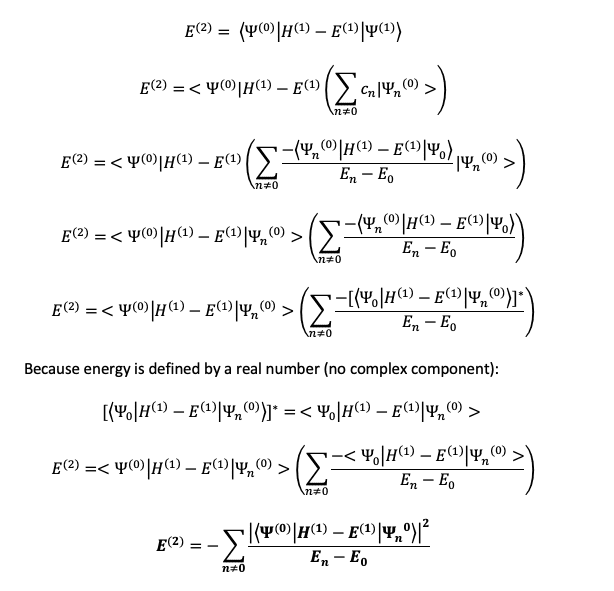
I'm struggling with the proof for the second order energy correction for perturbation theory when substituting in the first order wavefunction. I have attached an image of my current proof for it below, but I'm not sure whether this is the correct approach for it (the H's in the calculations below are hamiltonian operators)! I'm still quite new to using Dirac notation for these calculations so thought I should double-check it.
Cheers!