What is the nature of the described parametric curve?

[Duhoc]

x = r1cos(omegat) + r2cos(2omegat)
y= r1 sin (omegat) + r2 sin (2omegat)

1) Is this the equation of the graph of the curve in parametric form?

2)Do you have any idea what this curve looks like?

3)How would I determine the area inscribed by the curve at time t?

4)I don't know what ITEX means. Can you clarify?

Thank you,
Duhoc

 

[FrogPad]

x = r1cos(omegat) + r2cos(2omegat)
y= r1 sin (omegat) + r2 sin (2omegat)

1) Is this the equation of the graph of the curve in parametric form?

2)Do you have any idea what this curve looks like?

3)How would I determine the area inscribed by the curve at time t?

4)I don't know what ITEX means. Can you clarify?

Thank you,
Duhoc

I know I'm not halls. But what is omegat?

might be nice to learn latex, you can turn omegat into \omega t [/tex]

 

[Data]

You already have a thread; I don't know why you made a new one.

[ itex] allows you to use latex code inline. If you want things to look nicer when all you want on a line is math, then you can use [ tex].

Those equations certainly define a curve in parametric form. The "area inscribed by the curve" only makes sense for a closed curve, so you can't evaluate it as a function of t.

I've attached a picture of the curve plotted from t=0 to t=2\pi for \omega = r_1 = r_2 = 1.

 

[HallsofIvy]

1) Since those equations define a specific (x,y) for each t, yes, those are parametric equations for some curve.

As far as (2) and (3) are concerned, FrogPad and Data did a very nice job of answering them. Thanks, guys!

 

[jpr0]

I think this is how a solution should look. I'm really not sure of its correctness though, so if anyone would like to offer some feedback... I couldn't be bothered typing it into here, it would take too long, so I just attached a pdf.

 

[FrogPad]

1) Since those equations define a specific (x,y) for each t, yes, those are parametric equations for some curve.

As far as (2) and (3) are concerned, FrogPad and Data did a very nice job of answering them. Thanks, guys!

You thanked me for being a smart a_* to him :)
No problem. Anytime anyone addresses you specifically, I'll be sure to say something snide to them.

 

[Duhoc]

Solution

JPRO
Thank you for this beautiful solution. I will be off from work tomorrow and study it. Perhaps HallsofIvy might view it as well. I would be most interested in his analysis. As for frogpad, I don't think he was referring to me. In any case I'm not bright enough to be snide. But there is a fine line between smart and smart aleck. But if you are really bright it doesn't make much difference to me even if you cross it.

Duhoc

 

[FrogPad]

JPRO
Thank you for this beautiful solution. I will be off from work tomorrow and study it. Perhaps HallsofIvy might view it as well. I would be most interested in his analysis. As for frogpad, I don't think he was referring to me. In any case I'm not bright enough to be snide. But there is a fine line between smart and smart aleck. But if you are really bright it doesn't make much difference to me even if you cross it.

Duhoc

oh no man... I wasn't really being nasty. I was just kidding around

I just thought it was funny how you addressed hallsofivy specifically. There are some BRILLIANT people on this board (hallsofivy is definitely one of them). Anyways... have a good one man!

 

[Duhoc]

jprO-your solution

I spent the morning with a PhD in mathematics who assured me that your solution was correct only because "jprO is not the kind of person who is likely to make errors." He had to rush off to work, although he promised to explain all of your calculations in detail at a later time. But putting the calculations aside for the moment, as I understand your logic, you indicated that in order for the expression to make any sense the radius of the second compass must be less than half the radius of the first, and additionally, the limits of integration i.e. the extent of the curve must be between 0 and 2pi/omega, where omega is the relative rate of rotation of compass 2 with respect to compass 1. I have a little difficulty imagining what this looks like for any set of radii and omega. As we have assumed that your solution is correct, would I be stretching the limits of propriety if I asked three more questions? (Read no further if the answer is "yes.")
1-Is there a solution for a third compass with a wheel tracing out the curve inscribed by compass 2 at some multiple of omega?
2-For any number of compasses tracing out the contour of the prior curve?
3-Could this expression, if it existed, be integrated to describe a three dimensional curve in 4 dimensional space time?

Duhoc

 

[jpr0]

Hi Duhoc,

I don't have much time at the moment, so I'll try and give you a fuller reply later. To visualize the curves you are describing there is a free tool for plotting graphs of functions, of raw data and so on. It's called gnuplot. If you're using win32 (windows XP say) then you can download it from here:

ftp://ftp.gnuplot.info/pub/gnuplot/gp400win32.zip[/URL]

If you're using a different OS you can look here for the relevant version:

[PLAIN]ftp://ftp.gnuplot.info/pub/gnuplot/[/URL]

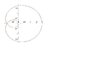
Just unzip the zip file, go to the "bin" directory, and run the binary wgnuplot.exe. This gives you a terminal. To plot the kind of curves you're describing you need a parametric plot, so type this into the terminal :

set parametric
pl cos(t),sin(t)

This will give you a circle (although it dosen't look like of the dimensions of the plot window, just readjust them). If you want to to plot the curve discussed above, try something like this

pl cos(t)+0.5*sin(2*t),sin(t)+0.5*sin(2*t)

Or if you want to see the plot of the first "compass trace" and then the second,

pl cos(t),sin(t) , cos(t)+0.5*cos(2*t),sin(t)+0.5*cos(2*t)

If you want to see how adding another compass ontop of the second looks try something like this:

pl cos(t)+0.3*cos(2*t) + 0.1*cos(3*t), sin(t)+0.3*sin(2*t) + 0.1*sin(3*t)

etc.. you can play around changing the radii here (the 0.1, 0.3 etc) and the angular frequencies.

To try and quickly answer your questions:

1) I don't see any trouble with this approach adding a third compass, it just increases the size of the expression for z(t). And it would have to be an integer multiple of omega so that the curve you trace out is closed. There should probably be some restrictions on how fast the angular rotation of the 2nd, and 3rd compass can be. For instance if you have the third compass whizzing round at 300.omega then it will start producing crossing points in the curve. I'll have a closer look to see how to derive what values of R and omega are valid.

2) Again I don't see any problem with adding more and more compasses, if you just work out what restrictions on the radii and angular frequency are. Probably the radii will get progressively smaller, and probably their sum shouldn't be more than R1, or some expression involving R1...

3) I'm not sure what the question is here. I'll re-read it later to see if makes any more sense.

 

[Duhoc]

duhoc-reply

Question three may not follow from the others. But I will try to clarify. Let's say I step into a vat of green paint. Dripping wet, I walk over to the wall, a white wall. I stand next to the wall with my hip and leg touching it. Without bending my knee I rotate my hip joint 45 degrees. I've traced a 45degree arc on the wall. My pants are still wet and I go to another spot next to the wall. I rotate my hip joint again, but this time a also rotate my knee joint. The inscription on the wall is different. This is in essence a description of the scenario you solved. And as you showed, the nature of the inscription is limited mathematically but also is of a specific varitey. Now, if the angular rotations were at an angle to one another then precisely the same principle would apply to 3 dimensional space. All we need to do is to imagine the green paint tracing out the inscription in three dimensions over time. And, as my theory goes, all of matter and energy in the universe is really these angular forms resolved by a three dimensional telescopic grid (rather like 3-d) graph paper with respect to time. A 4-d universe coposed of 4 dimensional magnitudes which take familiar forms.

Duhoc

Duhoc