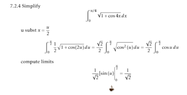- #1
karush
Gold Member
MHB
- 3,269
- 5
View attachment 9277
Ok I tried to follow an example but
kinda got lost in this
maybe more steps
the answer is from W|A
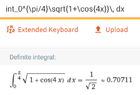
View attachment 9278
Ok I tried to follow an example but
kinda got lost in this
maybe more steps
the answer is from W|A
View attachment 9278