bolbteppa
- 300
- 41
Given Cartesian (x,y,z), Spherical (r,\theta,\phi) and parabolic (\varepsilon , \eta , \phi ), where
\varepsilon = r + z = r(1 + \cos(\theta)) \\\eta = r - z = r(1 - \cos( \theta ) ) \\ \phi = \phi
why is it obvious, looking at the pictures
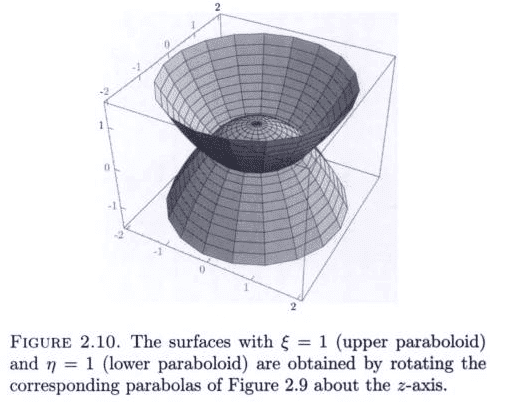
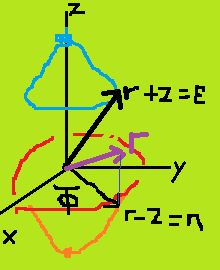
(Is my picture right or is it backwards/upside-down?)
that x and y contain a term of the form \sqrt{ \varepsilon \eta } as the radius in
x = \sqrt{ \varepsilon \eta } \cos (\phi) \\ y = \sqrt{ \varepsilon \eta } \sin (\phi) \\ z = \frac{\varepsilon \ - \eta}{2}
I know that \varepsilon \eta = r^2 - r^2 \cos^2(\phi) = r^2 \sin^2(\phi) = \rho^2 (\rho the diagonal in the x-y plane) implies x = \rho \cos(\phi) = \sqrt{ \varepsilon \eta } \cos (\phi) mathematically, but looking at the picture I have no physical or geometrical intuition as to why \rho = \sqrt{ \varepsilon \eta }.
\varepsilon = r + z = r(1 + \cos(\theta)) \\\eta = r - z = r(1 - \cos( \theta ) ) \\ \phi = \phi
why is it obvious, looking at the pictures
(Is my picture right or is it backwards/upside-down?)
that x and y contain a term of the form \sqrt{ \varepsilon \eta } as the radius in
x = \sqrt{ \varepsilon \eta } \cos (\phi) \\ y = \sqrt{ \varepsilon \eta } \sin (\phi) \\ z = \frac{\varepsilon \ - \eta}{2}
I know that \varepsilon \eta = r^2 - r^2 \cos^2(\phi) = r^2 \sin^2(\phi) = \rho^2 (\rho the diagonal in the x-y plane) implies x = \rho \cos(\phi) = \sqrt{ \varepsilon \eta } \cos (\phi) mathematically, but looking at the picture I have no physical or geometrical intuition as to why \rho = \sqrt{ \varepsilon \eta }.